Which waves are significantly different?
Editor's note: Michael Latta is executive director of YTMBA, a Myrtle Beach, S.C., research and consulting firm. He is also the associate dean, a professor of strategic marketing, and the Colonel Lindsey H. Vereen Endowed Business Professor in the Wall College of Business Administration of Coastal Carolina University.
Tracking studies are a staple of marketing research. They are especially popular when there are only two or three high market share competitors and the battle for market share is intense. The marketing research situation is complicated when product managers have a long list of key driver measures they want used to predict competitive performance variables like customer satisfaction, Net Promoter Scores or market share. Clients many times want to know if changes in individual key drivers are significantly different from wave to wave. There are ways to handle multiple measures of key drivers and a statistical test for change in key drivers, which are demonstrated here using an example for a biopharmaceutical.
When researching key drivers defined by attitudes, perceptions, beliefs and intentions regarding products like biopharmaceuticals, measurement and statistical issues can come into conflict. This conflict is caused by multicollinearity (high correlations among predictor variables indicating redundancy) and generates the need for data reduction (combining predictors to eliminate redundancy). Key drivers are many times measured by using rating scales. To increase reliability and validity of rating-scale measures, different questions about the same issue are asked. These different ways of asking about a key driver allow more reliable and valid measurement of key drivers like efficacy/safety, convenience, sales rep performance and expense/reimbursement in using biopharmaceuticals.
Sometimes as many as 27 measures used to define key drivers are used in a regression analysis predicting market share for a biopharmaceutical. Several of the 27 predictor measures may be so highly correlated with each other that they create a state of multicollinearity. In other words, a belief that “Product A sales reps are knowledgeable about the drugs they represent” may have almost identical answers to “Product A sales reps always provide credible information” and “Product A sales rep is responsive” – leading to very high correlations among three measures of the key driver “sales rep performance.” This redundancy is good for measurement and increases reliability. It is bad for multivariate regression analysis because high correlations among key driver measures cause what statisticians call multicollinearity. Multicollinearity causes the error term in a multiple regression analysis to be inflated, giving erroneous results in significance testing of a key driver such as sales rep performance to predict market share.
One way to handle multicollinearity is to use principal component analysis (PCA) to reduce multiple correlated measures of a key driver such as sales rep performance to a single principal component.
PCA is an effective option because it: uses the correlation matrix as input data to handle multicollinearity; maximizes the variance extracted in uncorrelated components; and it can be used to exactly reproduce the original correlation matrix and standard scores of the raw data if all components are retained.
In PCA, common variance, or variance shared among three or more measures, is indexed by an eigenvalue. Only the components with eigenvalues that represent common variance above 1.0 are used in further analysis since they represent those with a meaningful and significant amount of common variance (an eigenvalue is a measure of component strength and order of importance). The first component extracted has the largest eigenvalue and the last one has the smallest. These properties make PCA ideal for reducing a large number of key driver measures down to a smaller number of more meaningful and reliable principal components. The most stable and robust analysis utilizes the correlations among individual measures of a key driver in a principal component to create a more reliable way to predict market share.
There are two ways to approach PCA in this situation. The first is to use all key driver measures in a single PCA to see how the component structure that results follows key driver definitions. The second is to do separate PCA analyses for measures felt by product management to define a key driver that is distinct from other key drivers. The approach used here was to do separate PCA analyses for five groupings of key driver measures. The first approach was used in the demonstration below.
Method demonstration
There are five steps to the PCA multiple regression approach:
-
Calculate the correlations among all variables to be used in PCA.
-
Form composite key driver variables using the correlations in a PCA.
-
Generate linear combination scores for the key drivers from the PCA results.
-
Use these linear combinations in a multiple regression analysis to predict market share.
-
Test the significance of a key driver from wave to wave to see if there has been significant change in the key driver’s relationship to market share.
To demonstrate this approach, data from 27 key driver measures included in a survey of 125 physicians was used in the analysis for each of two waves. For the 27 predictor variables, PCA was used to extract five principal components underlying 26 of the original ratings. The last variable was kept as a separate predictor since it was considered to be a measure of the unique selling proposition (USP) for the biopharmaceutical.
After PCA, varimax rotation was used to simplify the columns of the component loading matrix. Varimax rotation maximizes the internal consistency of principal components and is the most commonly used approach many times being the default in analytic software like SPSS. PCA yielded five components and accounted for 76.7 percent of the variance in common for the 26 product/service attributes defining the five key drivers. The attributes defining the five components appear in Table 1.
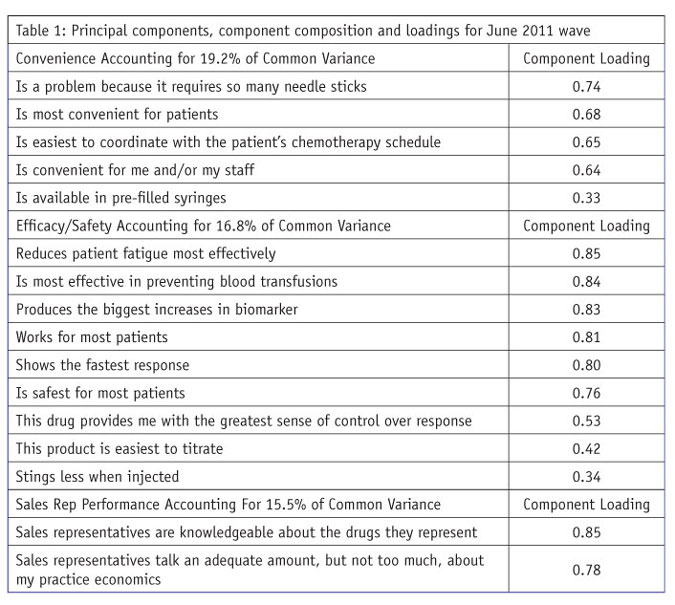
Following well-accepted rules of interpretation of PCA loadings:
-
the five components all have eigenvalues greater than 1.0;
-
each individual predictor variable appears on one and only one component;
-
a key driver measure is assigned to the component where its value is largest;
-
each component is defined by a minimum of three predictor variables; and
-
loadings defining a component are of sufficient size, larger than .30, indicating they are meaningful.
The components are named after the key driver measures that load highly on them. (For an excellent discussion of PCA and component analysis, see chapter 13, “Principal components and component analysis,” in Using Multivariate Statistics, 4th ed., by Barbara G. Tabachnick and Linda S. Fidell.)
The principal components are presented in Table 1 in descending order of their strength, with the strongest component listed first and so on to the weakest component. The same approach is used with the loadings (possible range of absolute values 0.0 to 1.0). Component loadings represent the correlation of an individual key driver measure with the key driver component. Component loadings also represent the contribution of the individual measure in the key driver definition.
Within the principal components procedure in SPSS, component scores can be generated representing linear combinations of the measures in a component to be used in multiple regression analysis. As pointed out earlier, the value of these linear combinations is that they are more reliable than raw scores and are uncorrelated with each other. The component scores for “convenience” are not correlated with sales rep performance or either of the other three components representing key drivers.
Both the principal components themselves and their loadings are arranged in descending order of size in Table 1. The single-item “unique selling proposition” measure is not included in Table 1 but is included in Table 2 as a key driver to be used in multiple regression. The results in Table 1 are for the first of two waves.
Multiple regression
The final analysis step for a wave of collected data was stepwise multiple regression to determine the value of the “convenience,” “efficacy/safety,” “sales rep performance,” “expense/reimbursement” and “familiarity” components and the USP in predicting market share. Stepwise multiple regression determines the relative size of the unique contribution of each predictor variable in relationship to market share. The analysis generates:
-
an overall test of significance of the ability of the key drivers to predict market share;
-
an estimate of variance in market share accounted for by the key drivers;
-
standardized beta weights for each key driver showing the unique contribution of each key driver to predicting market share; and
-
a standard error of estimate for each of those beta weights to be used in testing the significance of change in beta weights from one wave to the next.
The beta weights and their standard errors are needed for the wave-to-wave significance test. The R2 for the resulting model was .854, suggesting good accuracy using these six key drivers to predict market share.
The whole procedure of PCA, varimax rotation, component score generation and stepwise multiple regression was repeated for the December 2011 wave. Similar, but not identical, results for the key drivers were found in the second wave of data.
Testing differences between waves
The test for statistical significance is done to see if any observed difference in beta weights is big enough to be declared as having been caused by something other than chance. The calculations for significance testing can be done in Excel using a straightforward formula calculating a t-test. This t has [(n1 + n2) – 4] degrees of freedom and is calculated under the assumption of homogeneity of variance from one wave to the next. The ratio of the difference in beta weights to the pooled, or average, standard error calculates the t-test for significance testing. The formula is:

The degrees of freedom, 246, result from four standardized parameters, two beta weights (b) and two standard errors (SE), being estimated from the data rather than known in advance.
The applied statistics literature has suggested using Z, but since the beta weights and the standard errors are standardized to the same scale, we can assume homogeneity of variance and use this simple t-test with a large or small sample approach. (See “Using the correct statistical test for the equality of regression coefficients” [Paternoster, Brame, Mazerolle and Piquero, 1998] in Criminology, vol. 36, no. 4, pp. 859-865, for a complete discussion of the issues surrounding this type of statistical testing used widely in criminology. Or, in Statistical Methods [Snedecor and Cochran, sixth edition, 1967], pp. 432-436, “Comparison of regression lines,” an example involves age and concentration of cholesterol in blood serum in women from Iowa and Nebraska and uses the f-test instead of t for significance testing.)
With a sample size of 120 or more, a t-test critical value that must be exceeded is ± 1.96 and is used in a two-tailed test. So a calculated t larger than 1.96 regardless of sign is declared to show significant change from wave to wave. In the example in Table 2, the difference in market-share relationship to efficacy/safety, sales rep performance and USP all show significant change from Wave 1 to Wave 2 (indicated by an * in Table 2).
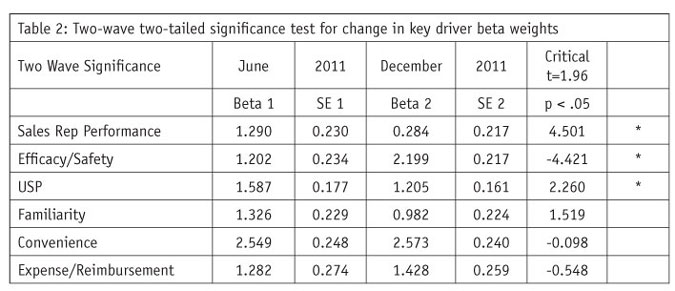
Table 2 indicates the key driver of efficacy/safety increased in effect on market share while the influence of sales rep performance and USP decreased in effect on market share. This may have been due to a market event such as an FDA-announced safety issue or a new competitor entering the market. No significant change was found for key drivers familiarity, convenience and expense/reimbursement.
Easily adapted
This statistical testing approach can be easily adapted to key driver tracking studies in biotech, pharmaceutical or other industries. If your products are battling for market share and you need to make sense of data from your tracking studies, consider using principal component analysis to reduce multiple correlated measures of key drivers.
