Michael H. Baumgardner is vice president of Burke Marketing Research's Consulting & Analytical Services Division. Baumgardner has worked in the area of marketing research and statistics for over 10 years. He has a Ph.D. and masters degree from Ohio State University. Ron Tatham is president of Burke Marketing Research. Tatham, formerly professor of marketing at Arizona State University and the University of Cincinnati, has worked in marketing research for over 15 years. His Ph.D. is from the University of Alabama. Both Baumgardner and Tatham have published extensively in marketing related books and journals. Burke Marketing Research is a division of SAMI/Burke.
Marketing researchers rely on tests of statistical significance to establish the reliability of observed effects (or lack of effects) in most studies. If Product X has significantly higher ratings than Product Y, then we are confident Product X is superior. If Product X has ratings that are not significantly different than from Product Y, we conclude the products are at parity. While significance testing plays an important role in marketing research, insuring that spurious effects will not lead to unfound conclusions, there are areas of research where tests of statistical significance can actually hamper our ability to make correct decisions.
Oatmeal cookie
To illustrate this point, consider the following scenario:
After great expense and many months of effort, a manufacturer has reformulated the recipe for its oatmeal cookie, giving them what they think is a better tasting cookie. The reformulation involves a change in a flavoring agent but has no impact on cost of manufacturing. They would like to introduce this reformulation, but only if it is indeed a superior product. A paired-comparison test is conducted among 300 cookie users and a test of statistical significance at the 95 % confidence level leads to the conclusion that there is no difference in preference. The dejected cookie makers go back to the lab to start all over again.
Consider the following: Assuming the reformulated cookie is really a superior product and would be preferred by 55% vs. 45% of the population, then:
1. Going into this test with the plan to test at the 95% confidence level, the researcher only had a 43 % chance of making a correct decision (and a 57 % chance of saying the new product is no better than the old). In other words, rather than conduct this experiment, the researcher would have had a higher probability of making a correct decision by flipping a coin!
2. If the researcher had gone into this study planning to ignore significance testing and simply say the product with a higher preference is the winner, (s)he would have had a 96% chance of making a correct decision. This correct decision would have led to production of a cookie with a 5% greater preference at no cost to the producer.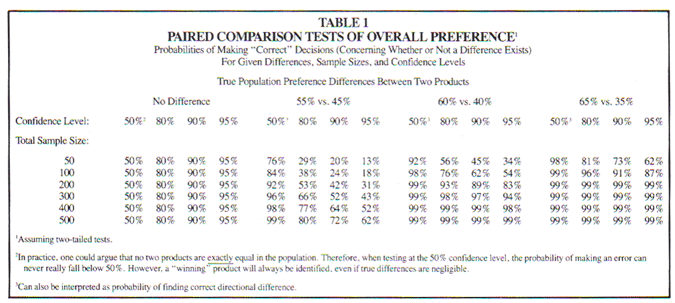
Making "correct" decisions
What went wrong? Table 1 provides probabilities of making "correct" decisions for given differences, sample sizes and confidence levels for paired comparison tests. Note that using, a confidence level of 50% is equivalent to doing no test of statistical significance at all; whichever product is higher in preference is the winner. What Table 1 demonstrates is that, given there is a difference between products, your best shot at correctly identifying the winner is by ignoring significance tests. Employing significance tests can too often lead you to conclude there is no difference between products when in fact there is.
What if there is no difference between products? In actuality, no two products are exactly equal in preference in the population. So "no difference" implies a "trivial difference." This being the case, the probability of making a correct decision regarding the superior product (even if the difference is trivial) can never fall below 50% if you ignore tests of statistical significance (i.e., you will always do at least as well as flipping a coin). If you were to employ a test of statistical significance, your confidence level is your probability of making a correct decision (if you equate a "trivial" difference with "no" difference).
Give some thought
The real moral to this story is that one must give some thought to the implications of a test of statistical significance before doing a test. It all gets back to Type I (concluding a difference exists when it does not) and Type II (failing to find a difference when one does exist) errors. You can greatly reduce Type II error by not doing a test of statistical significance. You may conclude a difference exists when it is trivial, and you may conclude the wrong product is a winner when the differences are trivial, but the probability of making a correct decision will stay above 50% if you ignore significance testing.
For this to be true for studies involving tests of statistical significance, you must first define what a trivial difference is. For example, if 55% vs. 45% is trivial, then we made a correct decision in the earlier example when we concluded there was no difference between products.
Defining not easy
Defining trivial difference is not always easy. If there is a large cost difference between manufacturing the current cookie and a potential reformulation, the increase in preference must be larger to compensate for the increased cost. However, if the cost difference is negligible, than any increase in preference may not be "trivial."
In any case, if you are willing to specify what trivial is, and you are willing to spend whatever is necessary to obtain the proper sample size, then you can control your probability of making a correct decision to any level you desire. Since, in practice, this does not happen very often in marketing research, one will probably run into situations where tests of statistical significance can be harmful to the decision making process. In such situations, one should feel free to ignore them.
