A response to William McLauchlan
Editor's note: Doug Grisaffe, Pd.D., is senior research associate, with Walker:CSM, Indianapolis, Indiana.
In the October 1992 issue of Quirk's Marketing Research Review, Dr. William McLauchlan presents a critique of the use of multiple regression analysis to model customer satisfaction (McLauchlan, 1992a). He argues that using regression to study determinants of satisfaction is, "fraught with both mathematical and philosophical dangers" (p. 10). However, it is my contention that, when properly applied, regression analysis is an excellent tool for use in customer satisfaction measurement (CSM) research. In fact, given the management objectives of CSM, multiple regression is a more desirable approach than the self-stated-importance approach advocated by Dr. McLauchlan. To support this position, I critique several points from his article, interspersing other relevant information about multiple regression along the way.
Dr. McLauchlan's hypothetical data
The hypothetical data Dr. McLauchlan uses to criticize regression are re-presented in Table 1. There are some characteristics of this hypothetical data set that should be pointed out. First, note that attribute B has no variation. Finding such an attribute in a real CSM data set would be a rarity. Naturally occurring individual differences in perception will lead to at least some variation in CSM measures. A second thing to note is the pattern of correlations for the hypothetical data. These correlations are also presented in Table 1. Note that attribute C correlates more highly with another attribute than it does with the overall satisfaction measure.
Dr. McLauchlan has illustrated the phenomenon known as "net suppression," a particular kind of suppression effect (Cohen and Cohen, 1978). Net suppression occurs when a predictor correlates with the dependent variable of interest, but to a lesser degree than it does with other predictors in the model. The phenomenon produces a regression coefficient with the "wrong" sign (and other coefficients with inflated magnitudes). Should the fact that suppression effects can occur in regression analysis cause us to throw out multiple regression as a CSM tool? I don't think so.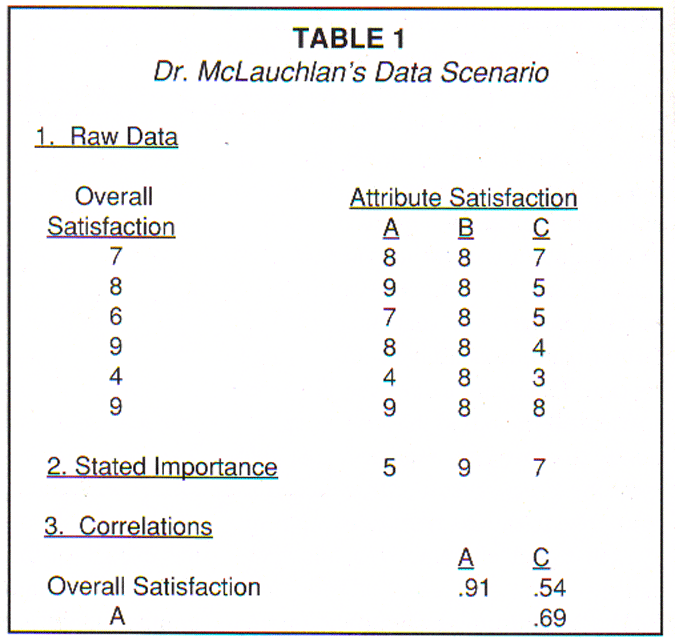
Statistical output will be only as good as the numbers that enter into it. It is true that problems like those described by Dr. McLauchlan might occur if a CSM researcher were to use post hoc statistical "fishing" to find the "right" regression model (e.g., stepwise regression), particularly if the modeling involved large numbers of redundant attributes as predictors. However, if a regression model has been specified correctly, a priori, with a parsimonious set of relatively distinct determinant attributes, each predictor should be more related to what it determines than to the other predictors. With sound research practices of that sort, suppression effects will be avoided.
Therefore, I contend that the problems Dr. McLauchlan demonstrates certainly may be avoided with application of a priori knowledge and sound research design. Later, I will have more to say about design issues.
Nonsignificant attributes with high stated importance
Dr. McLauchlan uses his hypothetical data to discuss an attribute having high stated importance, but a regression coefficient that is nonsignificant (nonexistent in his scenario). First, it should be noted that he provides arbitrary stated importances for the attributes in his example. They have no tangible link to the other hypothetical data.
Second, he proceeds to say that, based on regression, resources might be allocated away from that attribute. He notes how risky this would be given the high stated importance. But based upon regression, would resources really be allocated away from such an attribute? Not necessarily.
Consider the classic example of airline safety. When asked, most consumers would probably give very high importance ratings to safety. However, it would probably not be a significant predictor of airline choice. It is more of a minimum requirement, something that is expected and important but, does not contribute significantly to the prediction of choice as long as it exists to the necessary degree. Should we therefore take resources away from safety? No. It will be best to maintain current levels of performance, knowing that with less resources, performance could drop. As Dr. McLauchlan points out, this drop in performance could cause the attribute to become a differentiating factor, on which we would then have lower scores.
Therefore, the concern that Dr. McLauchlan points out is not an inherent problem with multiple regression as a CSM tool. Rather, it is an issue of correct managerial interpretation. Whether a measure of stated importance would be high or low, a nonsignificant regression coefficient should not be treated as a rote prescription for taking away resources. Usually in CSM work, the relative level of performance on an attribute moderates the interpretation of regression's information about significance as it applies to subsequent resource allocation.
Stated importance versus "derived importance"
The previous section points out that the degree of stated importance rated directly by respondents may not agree with what has traditionally been called "derived importance" (i.e., the degree of impact as identified by some statistical approach like multiple regression. I think the terms "determinance" or "impact" are more correct than "derived importance", but to be consistent with other literature I will use the derived importance label). This possible lack of agreement among the two approaches was implicit in Dr. McLauchlan's example of high stated importance and low (no) derived importance.
Given that the two approaches to importance can produce different outcomes, four possible combinations of stated and derived importance outcomes are presented in Figure 1. Dr. McLauchlan has discussed one cell of this table. To expand on this we must consider the other three possibilities.
There are two cells of the figure that show agreement between the two methodologies, and two cells of the figure that show a lack of agreement between methodologies. I have already dealt with cell 4 in discussing Dr. McLauchlan's example. Cells 2 and 3 pose no major source of conflict. The two approaches are in agreement, and with the exception of differences in degree and rank order of impact or importance, there is no disagreement about what is "important" and what isn't. That only leaves cell 1, where self-stated importance is low but regression's predictive impact is high.
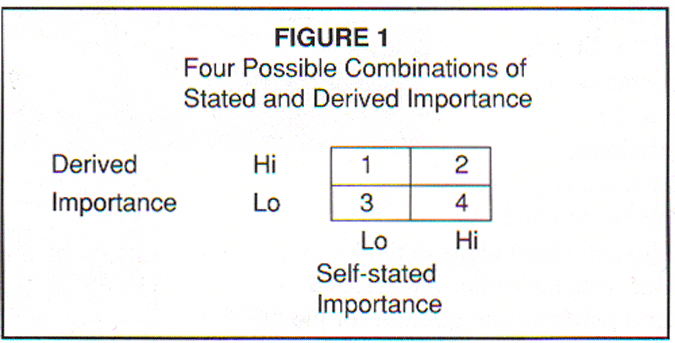
To consider cell 1, I borrow from some other writing of Dr. McLauchlan. In a paper presented at the recent Sawtooth Software Conference (McLauchlan, 1992b) he reasoned why derived importance based on multivariate techniques, including multiple regression, may produce better information than stated importance ratings if the context of the research involves strong image dimensions.
For example, consider a case where a sample of young urban professionals have rated post-purchase satisfaction with their BMW. Assume one of the attributes dealt with the "image" given off by driving a BMW. It is likely that many would not admit, in a self-stated importance task, that this image highly contributed to their purchase decision and subsequent satisfaction. However, in a correctly specified regression analysis, it is quite likely that such an attribute would have a large and significant regression coefficient.
As Dr. McLauchlan (1992b) has hypothesized, it is likely that the context of the research will point to the optimal method of arriving at "importance," and that there may be different methodologies that are more and less applicable to various research contexts. Given that, and given that this article aims at the specific context of CSM research, the next logical question is "which approach is best for CSM work"? Contrary to Dr. McLauchlan's position, I argue that "derived importance" is optimal for the quantitative components of CSM research because it fits CSM theories and management goals.
Regression fits CSM theories and management goals
One of the central ideas in CSM research is that retention of customers, and hence financial performance, is related to certain global attitudes/perceptions of products and services (overall quality, overall satisfaction, etc.). These global overall perceptions are a function of more specific, fine-grained perceptions. Typically, the more fine-grained components are measured as detailed attributes of products and services. The global measures are thought to be formed by respondents through some form of "cognitive algebra" where perceptions of the specific attributes are mentally "put together" to form the global perception. A basic representation of these ideas is given in Figure 2.

Given this basic framework, CSM researchers are interested in finding ways to increase scores on the overall measures. Higher overall scores imply that customers are more pleased with products and services, and hence more likely to remain as customers and generate revenue. Many corporations understand these principles, and are so committed to them that they financially reward employees who can bring about quantifiable gains in CSM measures.
What will be the most effective approach to influencing the overall measures? If we knew the "formula" that customers used to "put together" attribute ratings to arrive at their overall ratings, we could simply find those attributes that contributed the most. By making improvements on those actionable attributes with the biggest impact, we could optimize gains on the overall measures. But how can we find the formula that best captures how attributes are "put together?" Further, how can we make sure that no other formula will better explain the process?
Multiple regression is exactly what is needed. The technique provides a model of how the attributes get "put together." The regression equation combines all of the attributes into a single new measure which is as close as possible to the overall measure of interest. So, given the theoretical framework and the goals of management, the conceptual logic of multiple regression makes it highly appropriate as a statistical technique for modeling overall CSM measures.
Benefits of regression's best fit
Given the theoretical logic of attributes combining to form the overall rating, multiple regression provides a model of how the attributes get "put together". All other things being equal, making changes in those attributes will have specific quantified effects on the overall rating. No other model provides better explanation of the overall measure. To demonstrate this, consider the hypothetical data presented in Table 2.

Let us try various ways of combining the attributes to form the overall measure. It might be reasonable to think that respondents "mentally average" their perceptions of the attributes to arrive at their overall rating. This implies an equally-weighted average. With three attributes, each contributes one-third to the overall measure. The algebraic expression of this notion is demonstrated as follows:
MODEL 1. Equally weighted average:
Overall = .33*A1 + .33*A2 + .33*A3
A second model to consider, Model 2, expresses the notion that an averaging process still takes place in the minds of respondents, but that the attributes are weighted differently. For this example, the first attribute is given twice the weight of the other 2 attributes. The algebraic expression of this is:
MODEL 2. Differentially weighted average where
Attribute 1 has 2 times the impact of the other
two attributes:
Overall = .50*A1 + .25*A2 + .25*A3
A third model to consider, Model 3, expresses an unequally weighted combination where the "rule" for combining comes from multiple regression analysis. The equation is:
MODEL 3. Unstandardized regression model:
Overall = 2.61 + .14*A1 + .07*A2 + .20*A3
Table 3 summarizes the predictive accuracy of these three models. In addition, a very small constant (.02) was added and subtracted from the regression weights just to demonstrate that even minor changes in regression weights lead to worse prediction.

The conclusion from this demonstration is that no other way of deriving a weighting system for "putting together" the attributes will work as well as multiple regression's equation. Further, given that the equation has been correctly specified, increasing scores on the attribute with the biggest regression weight will produce the biggest gain in the overall measure.
Given CSM's theoretical framework and management goals, and what regression has to offer in light of them, we might ask how stated importance compares. While Dr. McLauchlan seems to hold up stated importance as a better alternative than regression, I contend the stated approach has several critical shortcomings relative to regression.
For one thing, self-stated importances offer no model of how the overall rating is arrived at by respondents. Secondly, any weighting system based on self-stated importances will provide more error of prediction for the thing we probably care most about influencing, the overall measure. Third, there is absolutely no assurance that increasing scores on attributes with the highest self-stated importances will provide maximized increases in the overall measure. In fact, based on the demonstration of regression's best fit, changes corresponding to stated importance will not maximize increases in the overall measure.
A note on regression and causality
Much of the preceding discussion, and the premise of doing regression with CSM data, implies that attribute perceptions combine to produce or determine overall perceptions. Clearly this involves the notion of causality, something Dr. McLauchlan warns is an "extremely dangerous proposition" (p. 12) for CSM research. However, I argue that multiple regression cannot be discarded on these grounds.
There is far more involved in the process of inferring causality than the choice of statistical technique. Several requisite conditions must exist. For example, there needs to be a sound conceptual/theoretical foundation in which plausible alternative explanations can be ruled out. Further, if X causes Y, X must occur before Y. Also, there must be an empirical association between X and Y. This last point is particularly important for the current discussion. While Dr. McLauchlan has correctly pointed out that "correlation is not synonymous with causation" , causation certainly implies correlation.
Consider the case of cigarette smoking and lung cancer. If smoking really causes lung cancer, then there needs to be some co-occurrence (correlation) of the cancer with smoking. The association needs to be viewed conceptually and theoretically so that we do not misinterpret the correlation by saying that lung cancer causes smoking. But, given the strong case for smoking as a cause of lung cancer, we certainly expect to find correlation. The question then becomes, given proper conditions for inferring causation, could we appropriately use multiple regression to estimate the degree of influence that smoking has in determining something like risk for lung cancer? The answer is yes. Regression can be used in studying causal processes.
Dr. McLauchlan is correct in stating that regression analyses "do not produce causal models" (p. 13), but the issue of causality does not rest in the choice of analysis technique. Simply using regression as a statistical procedure says nothing about causation. However, once one meets conditions for inferring causality, regression analysis most certainly can be used to estimate the magnitude of effects in causal models. In fact, the sociological and psychological techniques referred to as "path analysis" provide a rich and extensive history of using multiple regression to estimate effect sizes in causal models. Further, multiple regression can be used to produce estimates of causal effects from traditional experimental designs. These estimates can be shown to be exactly equivalent to those produced by the more standard analysis of variance (a tool often used in causal research).
So, again, we cannot rule out regression as a poor statistical tool for CSM simply for the fact that it does not inherently allow one to infer causality. Even very sophisticated approaches to causal modeling (e.g., use of LISREL) do not inherently allow causal inference. Statistical techniques cannot asses where the numbers come from. It is the researcher's job, regardless of the choice of statistical technique, to assess the plausibility of causality.
Thus, regression can certainly be used as a tool in CSM research, even to infer causality in those areas where it is justified. After all, if we cannot reasonably argue that improving the quality of various components and processes of our business will lead to higher ratings of the overall company measures we care about, what is the point of doing the research in the first place?
Good regressions from good design
Dr. McLauchlan points to "numerous other risks associated with regression-based approaches to satisfaction analyses" (p. 13). However, I argue that many of these risks are the result of poor data conditions rather than an issue of any particular statistical technique. Statistical problems more often than not will be ascribable to "messy" data that comes from a researcher's poor design rather than inherent shortcomings of analysis techniques like regression.
Let us consider two of the problems Dr. McLauchlan raises: multicollinearity and low R2 values. I would tend to question the design quality of a regression model with "20 or more regressor variables" (p. 12) that still had low R2 values. Further, with 20 prediction attributes, it would not be surprising to find multicollinearity.
I contend that good regression models come from good designs. Measuring many redundant attributes will of course produce multicollinearity. Even worse would be the use of stepwise regression in such a design to statistically "fish" for the determinants of the overall measure. That approach is notorious for capitalizing on chance.
Proper questionnaire design, based on good qualitative or secondary research and an in-depth understanding of the research context, is the best protection against low R2 values and multicollinearity. Having done one's design "homework", one can specify the "right" regression items based on sound management reasoning and the voice of the customer, not statistical fishing. Then, all the coefficients for that well-thought-through model can be estimated with standard multiple regression. The coefficients reveal relative impact among the items that are already known to "matter". In this way, one is already dealing with "high importance" items before even getting to the regression work.
Further, if the "right" items are determined a priori, questionnaire design is maximally efficient. To fish for the right variables after the fact implies that unnecessary items were included in the questionnaire, only to be tossed out after statistically discovering that they do not belong. With the right items included by design, R2 values will be sufficiently high to support the regression models. Finally, there will not be a need to conduct principal components analysis, especially if the attributes have been organized into logical groupings in advance. This will leave attributes at an actionable level so that managers know what to do when CSM analyses point to areas for improvement.
In summary, several of the "risks" Dr. McLauchlan assigns to multiple regression are linked more to issues of good design than the statistical technique itself. Again, there is an appropriate way to validly apply multiple regression to CSM analyses.
Should complexity prevent use?
Dr. McLauchlan presents a number of issues that need to be considered when running regression analyses (e.g., treatment of missing data, choice of modeling approach, etc.). He advises us "to consider the implications of the modeling technique" (p.13) before deciding to use it. I agree with thoughtful implementation practices. However, I do not believe the complexity of regression issues and considerations should necessarily lead us to a simpler approach like self-stated importance. The complexity of the statistical technique should not dictate whether or not it is appropriate. Instead, an analysis technique should be chosen because it is the best-suited tool to answer the research questions of interest.
We should not avoid the use of multiple regression in CSM work just because it requires thoughtful implementation. We would not advocate the use of aspirin to treat cancer simply because other treatments need to be carefully considered to avoid complicated drug interactions and side effects. Rather, we want careful and appropriate implementation of the most effective method for meeting the need. The analogy to use of regression in CSM is not trivial. As I have argued earlier, regression is ideal considering the theoretical framework underlying CSM research and the goals of management. Yes, there are many options and complex considerations with regression methodologies. But, in the hands of professional analysts, appropriate application of regression to CSM will validly address the key research questions and management objectives.
Concluding remarks
At a minimum, a company concerned about CSM will need to have a scorecard of customer-perceived performance on key business processes and attributes. These feed into more global overall measures that relate to retention of customers, and hence financial outcomes. Such measures of performance on key items can be obtained with sound research design. The measures then can be used to thoughtfully derive meaningful regression-based information, identifying areas that can be improved to obtain maximized effects on the global measures of interest.
Alternatively, there is the self-stated approach. Twice as many questions will need to be asked for each concept being measured: one for performance and one for importance. Given proper up-front design work, there will be little variation on the stated importance measures, thus limiting their usefulness. Further, making improvements on areas with high stated importance will offer no certainty about the impact, if there is any, on the global measures of interest. For these reasons, and all those described previously, this self-stated approach certainly seems less optimal.
While there may be some contexts in which stated importance is suited to the research questions at hand, I believe the research questions and management goals of CSM work make regression and its outputs a smarter and more powerful choice of analysis technique. By tracking performance and regression information across time, and implementing corresponding quality improvement efforts, one can monitor and influence the customer attitudes and intentions of interest. Management decisions based on such information, of which regression analysis is an integral part, can then lead to targeted gains in quality improvement and customer satisfaction, thereby increasing a variety of strategic and competitive business outcomes.
References
Cohen J. & Cohen, P. (1983). "Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences." Hillsdale, New Jersey: Lawrence Erlbaum Associates.
McLauchlan, William G. (1992a). "Regression-based satisfaction analyses: proceed with caution. " Quirk's Marketing Research Review, October, 1992, p. 10-13.
McLauchlan, William. (1992b). "The predictive validity of derived versus stated importance." Paper presented at 1992 Sawtooth Software Conference, Sun Valley, Idaho.
Thanks to Keith Chrzan and Lee Markowitz of Walker: Research & Analysis for their helpful comments on an earlier draft of this paper.
