Editor's note: Robert Kushner is a research consultant at Directions Research, Inc., Cincinnati.
Many times after survey data has been collected researchers have need to weight the results in order to provide a greater emphasis on a key variable or to adjust for sub-groups (strata) that have been over or under-sampled.
Additionally, the desire is to draw interviews from a population proportionate to certain sub-groups sizes. However, many times interviews cannot be placed into the appropriate strata until all the sampling has been performed.
When these instances occur, post-stratification is used to adjust the degree of influence each stratum has on the study results. Post-stratification of results involves the weighting of data after collection and is used many times by researchers when certain stratum may be over- or under-represented and results based on the total sample may be otherwise distorted.
When no weighting occurs, each respondent is "counted" once (i.e., each respondent receives a weight of one). When weighting is used to post-stratify results, the weight (or influence) respondents are given can be more or less than one. Following are some common examples of data weighting used for post-stratification purposes.
Examples
Quota to rep weighting
In the example shown in Table 1 the goal is to adjust the influence the respondents from each region have on the total. The weights to be applied reflect a ratio of the relative size of each region (in terms of the relevant variable, region population) and the actual region quotas. Thus, the goal is to offer greater influence to the larger regions and less influence to smaller regions. The weights are derived by taking the ratio of the "target" proportion of a region and dividing it by its relative proportion in the sample.
 |
For example, the weight for a respondent from Region #1 is calculated as 36.47/25 = 1.459. The weights in this manner are calculated and applied to each individual respondent so that one person in Region #1 is now counted as 1.459 persons; one person in Region #2 is counted as 0.779 persons, and so forth.
Many times only aggregate results are available so weighting on an individual respondent level cannot be conducted. In this case the weighting could be performed using the relative region sizes (% of total population from above table). An example of weighting the four regions together at an aggregate level is as follows:
The four-region average HH income is $50,250 (calculated by taking a simple average of the four region incomes). To allow the four regions to have influence based on population we take each regions relative proportion and multiply it by its average HH income. The sum of these four values produces the new, weighted average ($52,533), as shown in Table 2.
 |
Either weighting methodology (in aggregate or by individual respondent) alters the distribution of responses in total (i.e., across the four regions), but the distribution of responses in any particular region does not change. For example, weighting will not change the fact that 30 percent of respondents in Region #1 say they use Product Y. However, weighting will change the distribution of responses (the percent of all respondents that use Product Y) for the grand total across the regions.
Aligning a sub-sample to total sample
In another example, weighting is applied using a relevant variable collected within a survey. Awareness of a product was collected during the screening portion of a study; respondents were then terminated or allowed to continue based on other screening questions. After the study was completed, weighting was performed to bring the awareness level of the completed surveys in line with the awareness level derived from the total persons contacted for the study.
By making those respondents aware of the product worth 0.800 and respondents not aware worth 1.600, the total completed interviews are brought in line with the total contacts in terms of product awareness represented a weighted average based on contact awareness (Table 3).
 |
Population relative strata size is unknown
Another example of weighting data can be applied when a study collects responses using specific stratum quotas but their relative size in the population is not known. For example, a study for a new drug entailed interviewing patients with a specific condition. Quotas are set for each of four groups and respondents are randomly drawn from a common sample source. Questions are asked to classify patients into one of the four groups based on the patient's attitude toward their treatment experience. Interviewing a group is closed when its quota is reached (in this case n=50 for each group). For this study the question becomes, after all quota groups have been filled, how can we combine the four groups to obtain a look at patients as a whole when we do not know their relative stratum size in the population?
Before a quota group had been filled, we were accepting all completed interviews, regardless of which subgroup a patient belonged to (in other words, we did not reject a potential respondent because of which group they would fall in). However, after a quota group is full, we reject respondents that qualify for a completed group and only search for respondents to fill the remaining three group quotas. Therefore, before the first quota group is full, we are essentially taking a representative sample.
We can obtain a measure of the relative size of the four patient groups in the population by looking at the relative percentage of the completed group interviews at the point when the first group meets its quota (see Table 4 where Patient Group #2 has reached their quota before the others). Another option, if information is retained for all persons contacted, is to look at the distribution across the four groups after all groups meet quota, thus allowing a larger and potentially more stable number of cases on which to base the weighting.
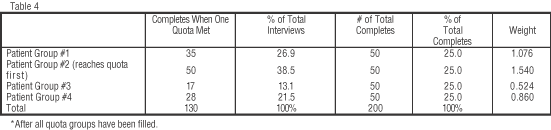 |
Applying the weights as calculated and combining the four patient groups can be a reasonable approach to looking at the data in total, absent other population information. However, it should be noted that weighting in this manner can be risky, given sampling error and therefore, should be used with caution.
Weighting and effective base
While weighting is an effective tool, the analyst pays a price if they decide to weight data. One way to examine the effect of weighting is by calculating the change of the base used in making statistical inferences (known as the "effective base"). The purpose of using the effective base when performing statistical calculations with weighted data is to reduce the likelihood of significant results simply because the weighting has made potentially large changes to the data.
The effective base is calculated using the following formula where ni is the number of interviews in strata i, ki is the weight applied to strata i, and h is the total number of stratum.
Effective base =
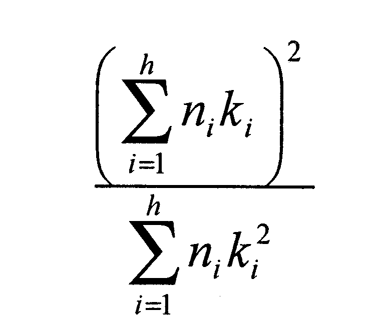 |
The effective base decreases as the relative difference of the weights applied increases. This produces a loss of efficiency compared to proportionate sampling.
Let's look at a simple example. A random sample of 100 respondents was drawn, and we receive 50 percent males and 50 percent females. However, to better fit population statistics, the sample should be more heavily female, so weighting is applied to achieve a 25/75 male/female split. The weight factors would be .50 for males and 1.50 for females. The calculations for the effective base is as follows:
| ((50 x .50) + (50 x 1.50))2 | = | 1000 | = | 80 (effective base) |
| (50 x .502) + (50 x 1.502) | | 125 | | |
Therefore, the result of the weighting plan "effectively" reduces the sample from 100 to 80 respondents (a 20 percent reduction). Given this, the effective base is one good criterion for evaluating your weighting plan. As a rule of thumb, the greater the magnitude of the weights, the greater the penalty incurred.
Another point of examination is that the penalty of post-stratification as opposed to stratified random sampling can be reflected by an increase in variance. A formula in William Cochran's, Sampling Techniques1, showing the estimated variance of a mean after post-stratification is as follows.
Estimated post-stratified mean variance =
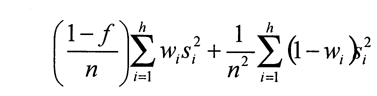 |
Where Wi = Ni/N (Ni=population stratum size and N=total across all stratum)
The first portion of the formula is similar to the variance formula below used under stratified random sampling (incorporating a finite population correction).
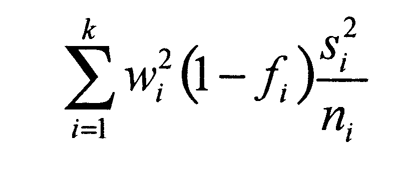 |
The second portion of the post-stratification variance formula is greater than or equal to zero and represents the "penalty" paid in terms of the increase in the variance. However, this increase could be small for large ni sizes.
Useful and necessary
Weighting is a useful and many times necessary tool. Many common statistical packages like SPSS and SAS offer weighting options that are easy to apply to data. However, use of this convenience should be tempered with experience and knowledge of any potential risks. For statistical testing, there may a penalty for using that may or may not be accounted for in the analysis in terms of an increase in variance.
In addition, weighting plans used to adjust the sample on a single variable will have much less potential to change results than a complex multi-variable weighting plan. Such severe weighting can alter data in ways that may be invisible to the researcher and may even change the conclusions that are drawn. Therefore, one should always balance the need to weight data with the knowledge of the potential effects.
References
1 Cochran, William, Sampling Techniques, John Wiley and Sons, 1977, p. 135.
