Editor’s note: Tony Babinec is a market manager at SPSS Inc., a company that writes and markets software for market research and analysis.
A common research situation is the need to predict a response variable based upon a set of explanatory variables. When most of the variables in the analysis are quantitative, including the response variable, then multiple regression is a popular technique. However, market researchers often work with variables whose values represent categories.
Predicting a dichotomous response
It is often the case that the response variable is dichotomous. Examples include:
- A direct marketer does a 20,000-piece mailing and gets 500 returns. The question is: what distinguishes those who responded from those who didn't?
- An Army recruitment office makes a re-enlistment offer to two-year enlistees whose terms are up. What distinguishes those who re-enlist from those who do not?
- A college admissions office wants to ensure that the entering class is of a certain size. What distinguishes students who accept admittance from those who do not?
In each of these instances, the response is dichotomous.
In practice, multiple regression is sometimes used in dichotomous response modeling. However, when the response variable is dichotomous, naive use of multiple regression might not be appropriate. This is because the assumptions under which regression is valid are not met.
Use of regression assumes that the residuals have a constant variance. However, when the dependent variable is dichotomous, this assumption is not met.
Use of regression assumes that the residuals are normally distributed. Again, when the dependent variable is dichotomous, this assumption is not met.
Use of regression assumes that the predicted values from regression will to some degree approximate the values of the response variable. It is convenient to code the response variable 0 or 1. Then, one might hope that the predicted values fall in the interval from 0 to 1, with predicted values near 0 indicating predicted membership in group 0, and predicted values near 1 indicating predicted membership in group 1. However, the predicted values from regression are not bounded, and thus are not guaranteed to lie in the interval from 0 to 1.
These problems are especially troublesome when the response variable is skewed, that is, one response category contains the bulk of the responses. In direct marketing, for example, a successful mailing is considered to be one with a 23 % response rate. That is, for every 100 letters mailed, the direct marketer gets 2 or 3 responses. In this instance, multiple regression should be discarded in favor of other, more appropriate techniques.
Some researchers turn to discriminant analysis in this situation. Discriminant analysis is appropriate when the response variable is categorical with two or more categories and the explanatory variables are quantitative. Discriminant analysis is used to determine which explanatory variables-and with what weight-can be used to distinguish membership in different response categories. However, discriminant analysis is not an ideal prediction technique, and moreover, when the response variable has two categories, discriminant analysis and multiple regression are formally identical. Thus, the objections to regression in this case also hold for discriminant analysis.
Finally, older AID and SEARCH programs likewise fall into the regression framework. They are designed for quantitative response variables although practitioners use them on dichotomous response variables. The objections raised for regression also hold for these programs.
What about categorical predictors?
Regression and discriminant analysis are even less appropriate when the explanatory variables are also categorical. Nonetheless, this situation is commonly faced by market researchers and survey researchers who use such variables as region, ZIP code area, sex, race, and the like, to predict a categorical response variable.
Statisticians have developed techniques such as logistic regression and logit analysis for the situation when most or all of the variables are categorical. Despite their appropriateness, these techniques have the drawbacks of complexity and difficulty in interpreting results. Fortunately, there exists a technique in the loglinear analysis family that is easy to use, produces intuitively appealing results, and is statistically valid- namely CHAID analysis.
Benefits of CHAID
CHAID stands for CHi-square Automatic Interaction Detection. "Chi-square" is the statistic used in categorical models; "interactions" are associations between variables which should be taken into account for successful prediction; "detection" is what the researcher hopes to do; and "automatic" means that a guided technique is available. The following list includes some of the benefits of using CHAID in response modeling.
The researcher often has a large collection of prospective explanatory variables. CHAID can be used to pre-screen data to exclude extraneous variables, that is, those with no predictive utility. In addition, the order of entry of variables which do enter CHAID conveys information on their predictive importance.
Simply because a categorical variable consists of a set of categories, it does not follow that each of those categories is behaviorally distinct in the response variable. CHAID can be used to determine which categories can be combined. For example, a data file might represent regions by 12 categories, but there might be only 3 different response patterns across the 12 regions. In this case, region categories ought to be combined. CHAID will perform statistical tests and combine non-distinct categories.
Some explanatory variables might consist of unordered categories, while others might consist of ordered categories. The researcher might wish to combine any categories of the unordered variable, if statistically appropriate, but only adjacent categories of the ordered variable if statistically appropriate. CHAID will do either.
Regression finds linear patterns. For example, suppose that as respondent education goes up, the percentage who say "yes" to a response item goes up. This pattern is linear, and regression will detect it. But suppose that as respondent education goes up, the percentage who say "yes" to a response item first increases and then decreases. Then, naive use of regression might miss the obvious relationship between response and education level because it is not linear. On the other hand, CHAID reveals non-linearities.
Regression finds main effects. That is, the effect of an explanatory variable is assumed to be constant across values of other explanatory variables. However, reality can be otherwise. That is, before the researcher can ascertain the effect of an explanatory variable on a response, the researcher might need to specify the level of some other explanatory variable. This is termed a "specification effect" or an "interaction." CHAID will reveal interactions in the explanatory variables.
CHAID produces a classification tree. The researcher can read down the classification tree to spot segments that are statistically distinct in response. Because CHAID uses Bonferroni adjustments in its built-in statistical tests, the segmentation model found in a set of data will tend to cross-validate well in a similarly drawn sample.
An example
To demonstrate CHAID, we chose some variables from the 1984 General Social Survey, a survey of the general adult American population conducted by the National Opinion Research Center. The response variable is opposition to abortion in the context where carrying the child to term could seriously endanger the mother's health. In the sample analyzed, 10.6% of the respondents oppose abortion in this context, while the remaining 89.4% favor abortion in this context. The set of possible predictors consists of:
- grouped age, a 3-category variable consisting of 18 to 32 years old, 33 to 52 years old, and 53 to 89 years old;
- attendance of religious services, a 9-category variable ranging from never to more than once a week;
- number of children, a 9-category variable ranging from none to eight or more;
- education level, a 3-category variable consisting of less than high school, high school, and more than high school;
- marital status, consisting of 5 categories;
- race, a 3-category variable consisting of white, black, and other;
- sex, a 2-category variable.
In the analysis, the categories of the attendance variable are treated as monotonic, so that only adjacent categories will be combined if statistically possible. On the other hand, the other variables are declared "free" so that any categories can be combined if statistically possible.
The CHAID analysis produced the classification tree shown in the accompanying figure.
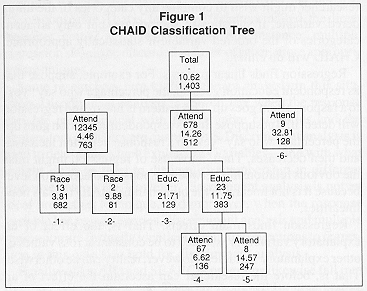 |
Reading down the tree, attendance is the most important predictor. Note that categories 1 through 5 of attendance are combined, categories 6 through 8 are combined, and category 9 is distinct. An important property of CHAID, not held by other AID approaches, is that it is not restricted to binary splits. Here, it split attendance into 3 groups. Note that the response variable trends upward across the groups: infrequent attenders oppose abortion when the woman's health is seriously endangered at a rate of 4.46 %; more frequent attenders (up to "weekly") oppose abortion at a rate of 14.26%; while frequent attenders (more than once a week-Baptists?) oppose abortion at a rate of 32.81%.
The next split in the classification tree reveals an interaction effect. That is, if the respondent is an infrequent attender, then race of the respondent is the next most important predictor. On the other hand, if the respondent attends more frequently, then educational level of the respondent is the next most important predictor. When race is the predictor, racial groups "white" and "other" are combined because they are not statistically distinct in response. They are, however, distinct from blacks. When education is the predictor, "high school" and "more than high school" are combined because they are not statistically distinct in response. They are, however, distinct from those with less than a high school education.
Finally, CHAID splits attendance groups 6 and 7 from attendance group 8.
To summarize, CHAID segmentation analysis reveals 6 segments in the data. In rank order by response, they are:
32.81%-those who attend religious services more than once a week. 21.71%-more frequent attenders of religious services who have less than a high school education. 14.57%-those who attend religious services weekly and have at least a high school education. 9.88%-blacks who are infrequent attenders. 6.62%-those who attend religious services almost weekly and have at least a high school education. 3.81%-whites and others who are infrequent attenders.
A lobbyist, political consultant, or fund-raiser could make good use of such information in targeting segments for activity, or avoiding "deadbeat" or antagonistic segments.
Look what the CHAID analysis has accomplished! If presented with the above data, most researchers would perform some cursory analysis such as cross tabulating each pair of variables and leave it at that. In a multivariate sense, the input table to the CHAID analysis is a 2 by 3 by 9 by 9 by 3 by 5 by 3 by 2 table. How would one make sense of that? The CHAID analysis reveals important variables, extraneous variables, interactions, and categories that can be combined.
What's more, for the sophisticated analyst, CHAID gives information which can then be used in more formal modeling. The classification tree shows what variables to use in further analysis and what variables to discard. If the researcher is interested in more formal models, then variables should be recorded to reflect categories that were combined in CHAID, and then a logit model could be developed (in SPSS LOGLINEAR) with a RESPONSE mean effect, main effects of ATTEND, RACE, and EDUC, and interactions involving ATTEND and RACE and ATTEND and EDUC.
Conclusion
CHAID analysis is appropriate for categorical data analysis, which is a data analysis situation commonly faced. While we illustrated CHAID using a dichotomous response variable, the same analysis can be performed with response variables having 3 or more categories. CHAID has a natural place as an exploratory multivariate technique, and resides in the same family of techniques as loglinear modeling. Just as in the use of regression, one should measure and include important variables in the analysis in order to get useful, not to mention correct, results. Since the input to CHAID is really a multidimensional table, it is useful to have large sample sizes to get any sort of detail in the CHAID classification tree. Having said that, CHAID belongs in every market researcher's arsenal of analytic tools.
