Editor's note: Michael Lieberman is founder and president of Multivariate Solutions, a New York statistical consulting firm.
The Shapley value, named in honor of Lloyd Shapley, who introduced it in 1953, is a solution concept in cooperative game theory. To each cooperative game it assigns a unique distribution of a total surplus generated by the coalition of all players.
Basically, the Shapley value is the average expected marginal contribution of one player after all possible combinations have been considered. This has been proven to be a fair approach to allocate value. A player can be a product sold in a store, an item on a restaurant menu, a party injured in a car accident or a group of investors in a large real estate deal. It is employed in economic models, product line distribution, procurement measures for embassies and industry, market mix models and calculations for tort damages.
The Shapley value shows up in several popular marketing research techniques. Below, I will set out the ABCs of Shapley values and then lay out three common applications in marketing research.
Let’s look at a very basic case of the Shapley value. There are three players, A, B and C. When they enter a game, they add points to the score. The total point-value in the game is 10.
As Figure 1 illustrates, when the order of entry is A, B, C, A and B have contributions of four and C has a contribution of two. However, in the second round of the game, A has a contribution of three, while B is five.
In total there are six possible different orders of entry. If we play all six and take the average contribution of each player, we arrive at the Shapley value.
Now I will lay out common applications of the Shapley value in marketing research. The Shapley value makes a positive allocation of items or value to that which generates positive revenue. Marketing researchers can turn to this when looking to maximize flow. The value is quite useful as it yields the highly equitable solutions and thus provides several vital research measures.
Regression and brand equity
Let’s say that a major automobile company has a public relations disaster. In order to regain trust in its brand equity, the company commissions a series of regression analyses to gauge how buyers are viewing its type of vehicle. However, what the company really wants to know is how American auto buyers view trust.
Since the disaster is so fresh, the company would like a composite of which values go into consumer trust across the industry. First, we would survey 10 of its major competitors on various elements of automobile purchase. We would then stack the data into one dataset and run a Shapley regression. What we hope to see are the major components of trust (Figure 2).
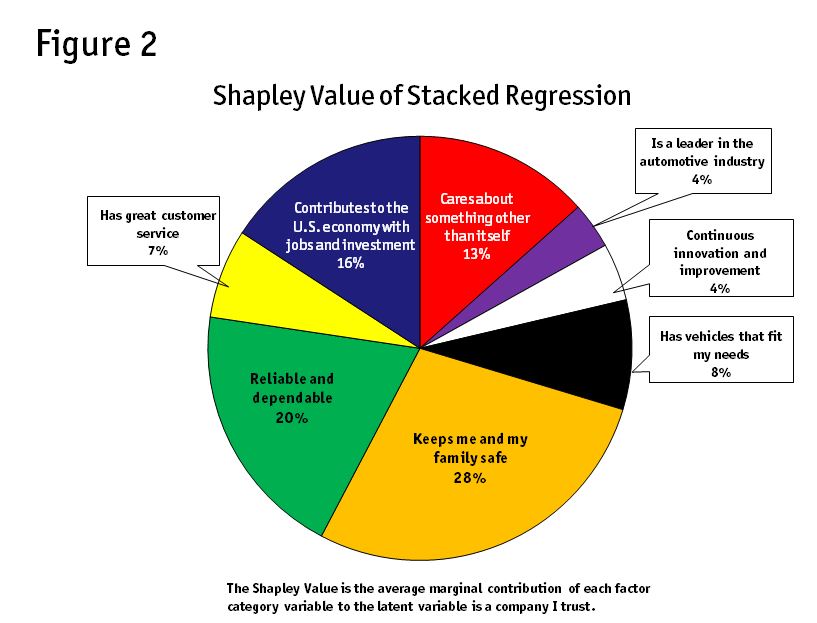
Not surprisingly, family safety is the leading driver of trust. However, we now have Shapley values of the major components. These findings could be handed over to the company’s public relations team that is working on damage control.
Product design
The Shapley concept of relative importance comes from product design, where we are able to piece together components in any way we wish. Products are bundles of attributes and attributes are collections of levels. I will take a typical conjoint study to create a product design example.
An energy drink company is looking to find out how to best configure a package with attributes such as the number of cans in a bundle, size of ounces in a can, amount of caffeine, flavor and price. By systematically varying these attribute levels according to an experimental design, it can generate descriptions of a hypothetical energy drink that are presented one at a time to respondents, who rate their preferences for all the product configurations.
In a conjoint study, relative importance is defined as the percentage contribution of each attribute. We take the sum of the effects of all the attributes to get the total variation and then we divide the effect of each attribute by the total variation to get the percent contribution. The attribute with the largest percent contribution is where we have the most leverage. This is, in effect, the Shapley value. The Shapley values for three different customer bases are shown in Figure 3.
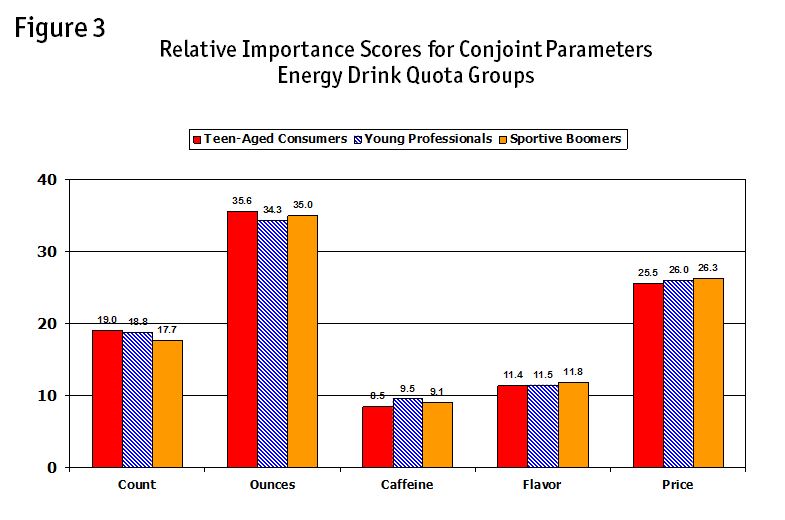
Changing the number of ounces in a bottle is the biggest impact on the likelihood of purchase. Price is way up there too, with a Shapley value of around 25 percent. Flavor and strength (caffeine) are really secondary factors in purchase intent but they still matter.
Maximizing on product lines
In the final example, I will demonstrate how to use a Shapley value to maximize product lines displayed in a store. Adding the right combination of new items will grow your business, while introducing the wrong new items will result in no growth – or even cannibalize your top performers, leading to a revenue decline.
Perhaps a supermarket chain, Gigantic Market, wishes to determine the maximum number of laundry soaps it should display. The first thing to do is deploy a maximum difference (max-diff) choice exercise. For purposes of illustration, let’s say that Gigantic Market has 28 brands to choose from.
Take the 28 brands and divide them into seven questions of four products. That way, each respondent sees each brand once. Below is a sample question from the max-diff.
Of the laundry brands shown below, which are you most likely to purchase and which are you least likely to purchase?
- Woolite
- Wisk
- Cold Power
- Daz
The beauty of this analysis is that we can create many different splits (a split is the seven-choice question) in random order so that each respondent sees a different set of questions. This is performed using a random-design Excel macro. If the sample is made up of 2,000 respondents, we may design 200 splits so that each is seen 10 times. We could, if requested, design a split for each respondent but it is generally not necessary.
The max-diff exercise yields a data structure in which we can calculate a Bayesian coefficient using logistic regression for each brand for each respondent. The coefficients are then normalized across each respondent. That is, the sum of all brand coefficients equaling zero for each respondent. Thus, some are positive and some are negative.
In a nutshell, we review the likelihood of purchase. If we take the average across the entire sample of the coefficients, we get the average contribution of each brand to the store. That is the Shapley value.
Figure 4 shows the Shapley value for each of the 28 brands. Brands in blue are positive and brands in red are negative.
Once the Shapley value is calculated, we simply choose brands that add a positive revenue stream to the product line. Those in red that are near zero such as Surf and Persil may be added to the inventory if Gigantic would like to sell 14 brands. We would tell Gigantic Supermarket to stock the brands in blue.