Editor’s note: George Butler provides modeling and scoring services through Iona Investment Corp., Redwood City, Calif.
If you think of regression modeling as unfathomable or if you had a hard time with high school algebra, this article is for you. For the others, it couldn’t hurt.
Indulge me for a bit and imagine that you are given a database containing the age and income of each resident in a certain neighborhood. Your boss requests that you use this data to come up with a model for that neighborhood to estimate someone’s income using their age as a predictor. An urgent call goes out for stalwart statistical help in the form of a certain Dr. Sigma over at Information Systems. Fortune smiles, the doctor is in. Doc Sigma wisely assures himself that there are no extreme values of income in the data to warp the analysis. Then he works his magic and presents you with a bona fide mathematical model: “Multiply the age in years by 971.4 and add 1536.2 and you get annual income in dollars. That’s your model and it’s optimal.”
You are duly grateful to Dr. Sigma and get to work on a report for your boss. You use the formula to graph income vertically versus age horizontally and admire the economy of this rule relating age to income. It’s a straight line - and an optimal one, at that. The glow dims somewhat when you see that the model estimates the income of 18-year-olds to be $19,021. (These youngsters should still be doing homework, not racking up that kind of dough.) The luster vanishes completely when you see that the estimated income for 70-year-olds is $69,534 and that each additional year of survival means an automatic $971 boost (hardly accounted for by Social Security cost-of-living adjustments).
Why is Sigma’s formula fishy? Because it’s a poor model. How could it be a poor model when it is “optimal?” It is optimal only if Sigma’s assumption about the shape of the model is correct. He assumed that the correct shape was a straight line. The computer did its part by finding a best-fitting straight line of all possible straight lines, employing a revered technique harking back to Karl Gauss (1777-1855).
Catch-22
If you sense that there is a Catch-22 here, you are right. If you knew the correct shape beforehand, you wouldn’t have much need for Doc Sigma. Doc didn’t know the correct shape either, so in a busy moment he did the convenient thing and presumed that it was a straight line. The equation for a straight line has the look of science but, in this instance at least, none of its substance. Straight lines often capture marvelous physical laws in science and engineering but there is no reason to be assuming them in commercial applications. An algebraic formula does have the virtue of simplicity and economy, but who needs an economical description of a poor model?
Surely the combined powers of mathematics and the Pentium chip wrested what was wanted from the data? Nope. What Doc did happens all too often because it is tempting to make casual use of a ubiquitous tool called linear regression.
Linear regression
The formula that Doc gave you multiplies age by 971.4 and adds 1536.2 to the result. He got the 971.4 and 1536.2 from linear regression software, which carried out the onerous computation needed to find these numbers. These numbers define a specific line that fits the data.
Linear regression is a mathematical method of estimating some quantity (such as a dollar amount) by “weighting” one or more predictor measurements, such as age, number of children, bowling average, and so on. It was developed long before the digital computer and its eternal reign is assured because of its appeal as an academic subject.
If the only modeling tool that Doc had on the shelf was a linear regression package we can see how his expedient model came about. Such packages assume that straight lines are the correct shapes relating each of the predictors to the quantity to be estimated. Suppose that, in addition to age, your data contained “number of children” as a predictor of income. Putting both predictors into the regression package would hatch a formula like:
Income = 1007.8*Age -752.35*Number of Children +933.6
The asterisk is a multiplication symbol. The impact of our newcomer, number of children, is also linear. That’s so because, totally independent of age, the estimated income drops, in straight line fashion, $752.35 with each additional child. We’ll use this formula relating age and number of children to income to illustrate what it is most important to know about the numbers that regression provides:
1) It is common, but misleading at best, to think of 1007.8 as a “weight” for age and -752.35 as a “weight” for number of children. If age had been expressed in months rather than in years, the new “weight” would be smaller by a factor of 12, simply to reflect the change of scale. The magnitude of the “weight” is therefore not a measure of the importance of the predictor that it is applied to. Call these multipliers “coefficients” instead, and you’ll be absolutely correct and avoid the semantic danger of “weight.” There will be as many coefficients as there are predictors in the model.
The only purpose of the coefficients and, indeed, all numbers (technically, parameter values) produced by regression, is to make the formula fit the past data well.
2) Note that the coefficient (-752.35), the multiplier for number of children, is negative. This must not be interpreted to mean that as the number of children goes up the estimated income must necessarily go down in the real world. The sign of the coefficient will only have a trustworthy directional meaning when there is just one predictor. If there are two or more predictors and they are correlated, one predictor can end up with a positive coefficient and the other with a negative coefficient to confound common sense. For our data, in fact, if number of children had been the sole predictor it would have gotten a positive coefficient! Combining number of children with age, with which it had some correlation, gave rise to the misleading negative coefficient.
3) The last regression parameter, the constant +933.6, exists to ensure that if each predictor takes on its average value, the resulting income estimate will also be the average. Linear regression always works that way. Given an average age of 45.67 and an average number of children of 1.41, we can plug these values into the regression equation as follows:
1007.8*45.67 -752.35*1.41 +933.56 = 45899
and 45899 is indeed the average income in the data. After the coefficients are multiplied by their predictors and summed, there will always be that constant (even if is zero) to add at the end.
Mathematical heroics
Thus far we’ve talked about linear regression’s assumptions of linear relationships and how to interpret the parameter values that it comes up with. But what if the relationship isn’t linear? You can toss the data into linear regression uncritically anyway, but what you will get is a linear approximation to the correct shape. The more the correct shape departs from flatness, the more accuracy you will lose.
Because the linear regression procedure is chiseled in classical granite, the burden of bending the data into something resembling a straight line falls upon the conscientious user. The technical word for bending is “transforming.” Because of his propensities, Doc Sigma would probably try something mathematical to do the transforming. For example, if age and income don’t have a straight-line relationship, perhaps the square root of age has a straight-line relationship with income. There is nothing magical about a square root. It is one of many mathematical functions that might be tried in an attempt to transform age into something new that will work better with linear regression. A transformation here and there might be fun and challenging, but what if you have a hundred or more candidate predictors to deal with?
A 1995 book written for the direct marketing industry has this to say on the subject of transformations [our comments are in square brackets]:
“...it is also fairly easy to look at a scatter plot [a plot of individual data points, with the predictor plotted horizontally versus the variable being predicted vertically] of the relationship and determine if the relationship is linear or if the relationship needs to be straightened by the use of some transformation.”
The above statement is true if there are a small number of cases and the relationship is so strong as to be obvious to the eye. If there is a weak relationship buried in 50,000 cases, Sherlock Holmes, armed with his magnifying glass, couldn’t find it. A similar tack, with the same difficulty, is to plot the errors (“residuals”) of a linear model to look for obvious patterns of missed information. Recently we were shown a very slow (but dogged) computer program that tries one transforming equation after another, dutifully plotting each formula that it finds on the monitor. You literally could let this thing run all night. Such fanatical devotion to analytical functions is hard to justify because the end user, the one paying the bills, undoubtedly has no intuitive interpretation of any of them.
Let’s return to the original problem of predicting income using age. To illustrate our point, suppose that the following heroic model provides a better fit to your data:
Income = 46001 -exp(0.01355*(Age-46)**2)
Not a good bet to give your boss warm and fuzzy feelings. There is absolutely no meaning to the above equation other than that it is a smooth curve that happens to fit the data better than a straight line. Even more exotic equations can always be found to fit the data ever tighter. These curve-fitting exercises are not only devoid of meaning, they can overfit and engender a false confidence that something scientific is being accomplished. Complexity often masquerades as sophistication, form as substance.
Mundane heroics
Let’s begin with what a model is and what it isn’t. A model is just a set of rules to take you from what you already know to an estimate of what you want to know. Getting back to our original hypothetical problem, you want to go from what you know (age) in order to estimate what you want to know (income). There will be some error, of course, but you would like to be right on average, being neither consistently high nor consistently low with your income estimates for any particular age range. Any set of rules that accurately describes the relationship between age and income is a valid model.
You would be better off by constructing your own tabular model along these lines:
Age Income
18-22 $7,500
23-33 $25,000
34-44 $38,000
45-55 $58,000
56-60 $30,000
61-up $21,000
At least this table reflects the reality that students and retirees make less, on average. It may not be algebraic or optimal but it is a model, and a nice nonlinear one, at that. Here is the essential difference between Doc’s linear model and your pragmatic table. Doc’s equation is “global,” meaning that it will deterministically come up with an estimate of income for any age, from zero to infinity. If, through a data entry or programming error, the value of age plugged into the formula were 999, it would cheerfully estimate Income to be $971,965. Be aware that many mathematical expressions will project into the wild blue yonder without regret if they are given predictor values ridiculously far outside the legitimate range. It is not always easy to find mathematical expressions that bend with the data in all the right places within the legitimate range!
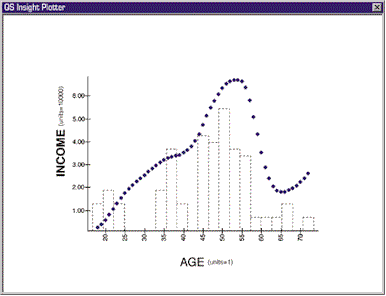
There is a more practical approach to this transforming business. It is suggested by the way we tabulated that the income for the 56-60 age range was about four times that of the 18-22 range - more or less by grouping contiguous age ranges and noting how the average income changed. The computer procedure for doing this is called local smoothing. In local smoothing it is assumed that in estimating, say, the income for age 35, ages 34 and 36 will have very similar incomes to those aged 35 and therefore get almost as big a weight in the averaging. The incomes for age 18 or age 70 would have no relevance to the 35-year-olds and get a weight of zero in the averaging. It is more sensible to use the computer to find this local information directly than to hunt for a shape (mathematical function) that will undulate fortuitously in just the right places. The figure illustrates the result of a local smooth.
 |
Categorical predictors
Linear regression assumes that the predictors measure something. Suppose that we have as a predictor marital status, and it is coded 1 = married, 2 = single, 3 = divorced, 4 = widow(er). These four numerical codes don’t measure anything; they are arbitrarily assigned to label the categories. The user of linear regression has to tap dance around this problem by the creation of additional predictors called dummy variables. We won’t get into all of that, but advise you to note that it is another awkward aspect of trying to accommodate to the assumptions of linear regression. We don’t envy anyone who has to deal with dozens of candidate predictors that require the transformation trick or the dummy variable trick.
Is the model significant?
In evaluating how good a model is, the only thing that counts is how well it predicts on data that it hasn’t seen before. Always hold out some data from the modeling process for that purpose. When the scores for the outside data are sorted from lowest to highest, do the lowest and highest scores obviously separate the opportunities from the risks? Comparing the discrimination of the lowest 10 percent of the scores versus the highest 10 percent of the scores is a common measure of goodness. There is nothing special about grouping the scores by deciles. A good rule of thumb is to make the groupings as small as possible while the pattern of gradual discrimination from group to group is preserved. If the gradation is obviously present and the result on out-of-sample data looks good enough for you to use, it is significant, period.
The ordinary semantic meaning of the word “significant” is “meaningful” or “important.” The statistical meaning of the word is a judgment that a departure from a hypothesis is too large to be reasonably attributed to chance. “Significant” in the statistical sense has nothing whatsoever to do with whether a result is good. It only has to do with the odds that the result isn’t random. Keep it simple: If it looks good enough for you to use, it surely is statistically significant and you will be spared expert advice of the following kind (from the previously-cited book):
“The ratio of model sum of squares divided by its degrees of freedom to error sum of squares divided by its degrees of freedom is the F statistic. If the p value is less than 5 percent, then the model is considered statistically significant with 95 percent confidence.”
Guarding the temple
If you look at linear regression as mathematics, it is beautiful. If you look at it as a tool for modeling and scoring it has many blemishes. To approach the mathematical temple you need a priesthood that knows how to manipulate the data to conform to the linear canon, talk about F tests, and issue these kinds of warnings (same book again):
“...we should keep in mind the fact that a final regression model may have to be applied to a customer file of millions of names, and the more complicated the model, the more difficult it may be for programmers, who are not statisticians, and who may not have the programming tools required to deal with logs, to score the database.”
This is an incredible statement. After all the folderol to get the model, the poor programmer may not have the wherewithal to use it!
Conclusion
There is much more to the subject of linear regression. We’ve offered the most practical tips because regression is everywhere and has so much tradition behind it that it will be around for a long time. Linear regression is a legacy of the pre-computer days and requires experts to service it properly. This is backwards and expensive. Software should serve people. If you really know what you want, you can render it in software. Modern, computer-oriented methods can take care of those linear regression strictures that now require a high-priced attendant, including the screening out of extreme values, performing transformations, and dealing with categoricals. When it comes time to predict, there is no reason why it cannot be done automatically and embody the ability to handle data that fall outside the range of the data used to build the model.
