Editor's note: Mike Fassino is managing director of Fassino Associates, a marketing science company based in Media, PA.
Readers of the Data Use column are by now familiar with the measurement of utility. Conjoint analysis has emerged as a powerful and widely accepted methodology for determining the perceived value of product/service attributes and the availability of software to assist with the design of conjoint tasks and the estimation of utility values ensures that an even wider audience will be attracted to these procedures.
The purpose of this month's column is not to explore conjoint analysis. It is to introduce market researchers to a technique known as Structured Equations Models (SEM). This technique is also frequently referred to as Causal Modeling and as Latent Variable Modeling. Some authors refer to these models as LISREL models, though LISREL is really the name of a computer program that performs structured equation modeling. In the hope of illustrating the managerial usefulness of these procedures, we will illustrate how they might be used to "get behind" the results of conjoint analysis to more fully understand the motivational, perceptual or psychological determinants of perceived value and thereby suggest strategies and tactics to manipulate consumers' perceptions of value.
An obvious "shortcoming" of conjoint analysis is that the utility values are static representations of preference. We have put the word "shortcoming" in quotations because we certainly do not view this as an inadequacy, it is just a limitation of conjoint analysis. The limitation is that the utility values are stripped of the psychological context in which they arose. We will present SEM as a way of reintroducing the psychological context, though other researchers view SEM in a far more general nature. Our discussion of SEM will be notably void of statistical and mathematical details and controversies (and they are many); instead it will focus on two very specific and practical applications. For the more general and technical developments, the interested reader is referred to the November, 1982 issue of the Journal of Marketing Research which was devoted entirely to structured equation models.
To motivate the discussion, suppose we had the following two data sets:
1. The part-worth utility values for three features of new automobiles obtained through conjoint analysis. Let these three features be Acceleration, Cost and Size.
2. Ratings of agreement or identification on a battery of 20 attitudinal, lifestyle and demographic data.
Our interest is in relating these two sets of data to each other. The traditional approach would involve some sort of regression analysis of the utility values onto the battery of agreement ratings. To avoid ambiguity in terminology, the battery of agreement ratings will be called independent variables and the set of utility values are the dependent variables.
If there was a substantial (and meaningful) pattern of correlation between the attitudinal items, we would probably first perform a factor analysis of these and then use the resulting factors as our independent variables.
Such an analysis would provide:
1. A set of weights indexing the magnitude and direction of the relationship between each of the independent variables and the dependent variable. We will call these regression coefficients.
2. A measure of the overall strength of the relationship between the two data sets. We will call this it-square.
3. The interrelationship of the items. We will call this factor loadings.
SEM grew out of this analytic tradition and it provides these three interpretive tools, but SEM also has 7 other attractive features that recommend its use in market research:
1. Adjusting the factor loadings and regression coefficients so as to maximize it-square;
2. Second and higher order factor structures;
3. Relational chains;
4. Decomposition of direct and indirect effects;
5. Sets of "dependent variables";
6. Assertion of causal relations between independent and dependent variables;
7. General models beyond OLS such as GLS, ELS and distribution-free regression.
The remainder of this article will be devoted to illustrating the first five of these features of SEM. Assertion of causality and general models require too much technical discussion to develop here.
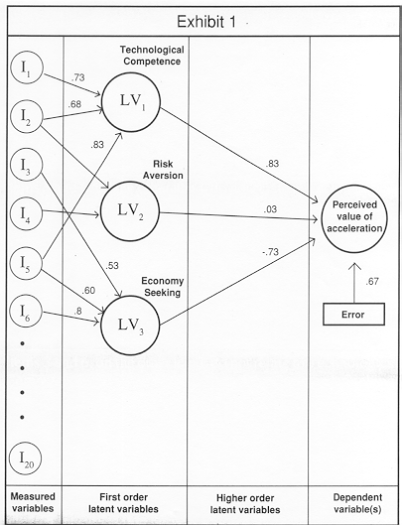 |
Exhibit 1 shows a set of hypothetical results around which we can build our demonstration. In this figure, the circles labeled I1 to I20 represent the twenty attitude and lifestyle questions. Each of these 20 items has an arrow pointing toward a column of circles in the middle of the figure. The circles in the middle represent latent variables (more on these later). Each latent variable, in turn, has an arrow pointing toward the dependent variable, in this case the perceived value (utility) of Acceleration. The dependent variable also has an arrow directed at it from a box labeled error. Each arrow has a number associated with it. The numbers from the items to the latent variables are analogous to factor loadings, those from the latent variables to the dependent variable are analogous to regression coefficients and those between the dependent variable(s) and error is analogous to it-square.
The results of SEM are almost always presented in diagrams of this type, known as Path Diagrams.
1. Latent Variables:
A latent variable is an unmeasured, holistic variable. It could be argued that items 1,2, and 5 are all different measures of the same underlying cognitive domain. The underlying cognitive domain is the latent variable. The numbers on the arrows between the measured and latent variables show the weight each measured variable carries in defining the latent variable, just like a factor loading. In our example, measured items 1, 2 and 5 all contribute substantial weight to the latent variable we have called Technological Competence.
In other words, these three items have a large correlation across respondents and we argue that this correlation is due to the fact that they all address some aspect of Technological Competence. (To be exact, the assertion is that the latent variable, Technological Competence is the cause of the observed pattern of high correlation between these items). Items 3 and 6, on the other hand, do not relate to Technological Competence, but to the third latent variable, Economy Seeking. So far, everything should be pretty familiar. We would derive names for the latent variables by looking at the items which contribute large weights, just as in factor analysis.
Now the arrows projecting from the latent variables to the dependent variable deserve special attention. This is the weight each latent variable carries in "driving" the perceived value of the dependent variable, Acceleration. The path diagram indicates that as the strength of respondents' association with the items that form the Technological Competence latent variable increase, so too does the perceived value of Acceleration. On the other hand, as their association with the items in the Economy Seeking latent variable increase, the perceived value of Acceleration decreases.
The arrow labeled error can be thought of as a measure of the overall fit of the model, analogous to an it-square value in regression.
This should all sound very much like the traditional approach where we first perform a factor analysis of the items and then use factor scores as the independent variables. But there is one very, very large difference between the traditional two step approach and the SEM approach: in the traditional approach the two steps, forming factors and regression, are completely independent. The correlation between items determines the definition of the factors-and this correlation is entirely independent of the degree of relationship between the items and the dependent variable.
In the SEM approach, the definition of the latent variables (i.e. the weight the items carry in defining the latent variables, the first set of arrows, the factor loadings) is adjusted so that the degree of relationship between the latent variables and the dependent variable is maximized. In the traditional approach, you would form your factors and then hope they explained a sizable portion of the variance in the dependent variable, using the it-square value as a measure of how well your hope was realized. With the SEM approach, the very definition of the factors is achieved so as to maximize the amount of variance explained in the dependent variable. Two important implications of this iterative, variance-maximizing approach to forming factors are:
- The interpretation of the latent variables in an SEM analysis are generally clearer and more unequivocal than in factor analysis;
- The resulting latent variables are more managerially actionable since they are defined with explicit reference to the dependent variable.
2. Second and higher order factor structure:
In factor analysis, the factors are always uncorrelated: the relationship is between the items and the factors, there is no relationship between the factors themselves. In the SEM approach, there can be very rich patterns of relationship between the latent variables. In fact, it is common in SEM to find "higher order factors."
Let me give an example of a higher order factor that will also drive home the distinction between the SEM and the factor analytic approach. Suppose we gave a group of children a test in which there were several algebra problems, several science problems and several problems which tested the students' ability to analyze and organize reading material. In such a test, we are likely to find very high correlation between all the algebra items-a student who solves one will likely solve many others. Similarly, we are likely to find a high correlation between all of the reading comprehension items. If we performed a factor analysis of these data, we would find three factors: Mathematical Ability, Reading Comprehension and Science Ability (see Exhibit 2).
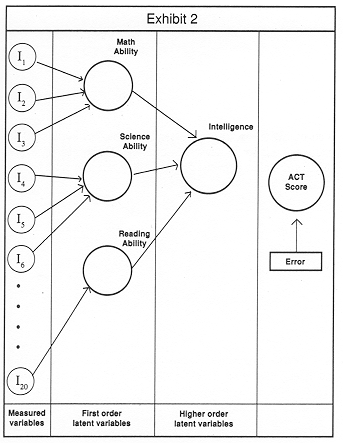 |
These three factors would result because there would be a very high degree of correlation between all of the questions tapping a specific discipline. If we did this analysis using SEM, we would also come up with these four factors (but we would call them latent variables). But in factor analysis, these four factors would be forced to be uncorrelated. That is, there would be zero correlation between a student's mathematical ability and science ability. That is just the way factor analysis works (even though you can end up with correlations after a rotation, the original extraction of the factors results in their mutual orthogonality).
If we instead used the SEM approach, we would most likely find that there is a discemible pattern of correlation between these four latent variables. We could then hypothesize that these four latent variables are all different measures of some other underlying factor, in this case, intelligence.
Intelligence would be a higher order factor. The situation is depicted in Exhibit 2.
Now, if we had some other variable like ACT scores, we could set up the analysis so that the definition of the latent variables, and, therefore the higher order factors, best predict ACT scores! And rather, for instance, than all of the algebra items loading equally onto the Mathematical Abilities latent variable (as would be the case in factor analysis), we might find that those that deal with trigonometry have a greater weight than those that deal with fractions, the implication being that a student's ability in trigonometry is a better predictor of ACT scores than their ability with fractions. Thus, if we wanted to impact ACT scores, we should provide remedial education in trigonometry. Extensions of this line of thinking into marketing should be evident.
Higher order factors deserve greater recognition and attention among marketing researchers. It may well be the case that advertising's effect is on higher order factors rather than individual items. Standard methodologies which show advertising to be ineffective may be addressing the wrong level of the hierarchy. Moreover, it is known that consumers process and assimilate information into chunks or clusters; each chunk would correspond to a higher order latent variable.
3. Relational chains:
A hierarchical pattern emerges in SEM: if you have several measured items with a stable pattern of correlation, you will get a latent variable. If you have several latent variables with a stable pattern of correlation, you will get a second order latent variable. If you have several second order latent variables with a stable pattern of correlation, you will get a third order latent variable, etc. Each successive level of this relational chain results in latent variables of greater abstraction and generality than the level below, as intelligence is a more abstract but general concept than science abilities. Although increasingly abstract and general, higher order latent variables continue to be "tied" to the original items in two meaningful ways:
1. The pattern of relationship between the measured items is caused by the higher order variables;
2. The weight variables at one level of the chain carry in defining latent variables at the next order of the chain maximize the regression coefficients at each step along the chain.
This gives rise to an important idea we will return to below: at any given level of the chain, the variables one level below the current level are independent variables and the variables at the current level are dependent variables. This allows us to use sets of variables as the dependents, rather than a single variable, as is the case in regression analysis. More on this below.
It is entirely possible for a measured variable to have a strong relationship with a latent variable at some level, but only a weak relationship with the variables one level below. For instance, one might find that Respondent Income has a small and statistically negligible relationship with all of the 20 attitude items, but the relationship of Income with a latent variable (itself defined in terms of these twenty items) could turn out to be very large and statistically significant, since we would be examining the relationship of income with a more holistic aggregate.
One very promising application of SEM in marketing research involves modeling value chains in business-to-business marketing. Space prohibits a detailed discussion of this application, but we can outline the idea as in Exhibit 3. Here we show a value chain with four levels. At the first level, several firms produce material that are combined at the second level of the chain. Firms in the third level of the chain distribute the product manufactured at the second level (from components manufactured at the first level) to consumers at the fourth level.
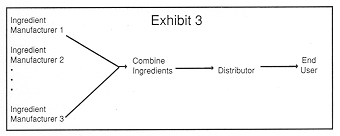 |
A model can be developed wherein each level of this value chain corresponds to a set of latent variables. In this example we would have first, second, third and fourth order latent variables. The degree to which each level of the chain "agrees" about the value of the various elements introduced at levels below it corresponds to differentials in the weights linking the various levels. The notion of "value adding" can then be put into an empirical framework-value adding occurs when consumers at a given level of the relational chain have a greater weight for a variable than consumers one link away. SEM, therefore, might help market researchers more meaningfully understand business-to-business marketing where there are several firms contributing to a product's final quality, and each firm has a different value structure, different levels of quality and service, different pricing, etc.
A formally similar problem results if you want to relate product features to a brand's self- and cross-price elasticity of demand coefficients. What we are saying, in short, is that SEM allows one to make a strong bridge between different portions of a survey or between different databases.
4. Decomposition of direct and indirect effects:
It may be the case that not all of a measured variable's relationship with the dependent variable is mediated through a first order latent variable. Everyone who has ever done a regression analysis with factor scores knows this, since whenever a regression coefficient is less than 1.0, this is potentially the case.
The point is that any independent variable (whether it is a measured variable or a latent variable) can have both direct and indirect effects on the dependent variable. In our example relating childrens' academic abilities to ACT scores, vocabulary would have two paths through which it effects ACT scores (See Exhibit 4). First, vocabulary would have an effect mediated through the Reading Skills latent variable. This is an indirect effect. Vocabulary would also have a direct effect on ACT scores, since the test assumes a level of familiarity with English. In other words, some of the relationship between Vocabulary and ACT Scores can be explained in terms of a child's Reading Ability (which itself can be explained in terms of intelligence) and some of the relationship between Vocabulary and ACT Scores is not explained by Reading Ability, but is unique and independent of Reading Ability. These are direct effects, effects not mediated by any intervening variable. Again, extension of this example to marketing situations should be straightforward.
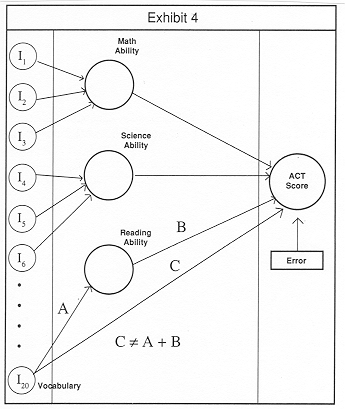 |
In the language of SEM, this is known as Effects Decomposition. SEM provides a rich set of procedures for determining the portion of a relationship mediated through some other latent variable(s) and the portion that is unique, both of which can be influenced by marketing tactics in different ways.
Taken together, the idea of direct and indirect effects and chains of higher order latent variables give a market researcher the ability to develop very detailed and sophisticated models of market response.
5. Sets of "dependent variables":
So far, our discussion has used only one dependent variable, ACT Scores or perception of value for a specific product attribute. This was just for simplification. Unlike regression analysis, where there is only one dependent variable, SEM provides the facility for having many dependent variables (as is really the case in the real world where preference, purchase intent, price sensitivity and brand loyalty are all interdependent, correlated dependent variables and all of the marketing mix are independent variables).
As already intimated, the notion of dependent and independent variables is not as rigid in SEM as it is in regression. Any variable can be either a dependent or independent variable, depending on how you want to think about a system of relationships. As mentioned, at any given level of a relational chain, the variables at that level are dependent variables and the variables one level below it are independent variables. (If we add two important concepts-directionality of effect and priority in time-the SEM models cease to be correlational and become causal models).
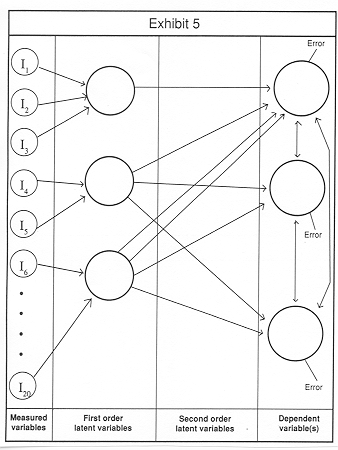
In our original example, we have three dependent variables, the three features of a new car studied with conjoint analysis. Using the traditional techniques, you would do three separate regression analyses with no real relationship between the individual results. SEM will solve for the regression weights of all three dependent variables simultaneously. SEM will also show you the relationship between the three dependent variables, something traditional regression analysis can not do (since there is only one dependent variable). This is illustrated in Exhibit 5 by the double headed arrows between the dependent variables, indicating that there is a correlation between each. (The observant reader will have guessed that a latent variable could be put "after" the three dependent variables to explain the correlation between them). And if one posits intervening latent variables between the measured variables and the set of dependent variables, SEM will define the latent variables so as to maximize the relationship with all three of the dependent variables, using both direct and indirect paths!
 |
Hopefully, this article will have suggested the versatility and power of SEM. It is important to note, however, that SEM is really a modeling system and not a data reduction methodology. This means that in order to build a higher order latent variable model with measured variables having both direct and indirect effects, one needs to have a pretty good understanding of how a marketplace is structured. SEM is best used for testing the relative adequacy of several competing models of how a market is structured, rather than for discovery how a market is structured.
Some of the ways we have used SEM include:
1. Using conjoint analysis derived utility values as the dependent variable and attitudinal items as the independent variables to determine how association with the attitudinal variables "drive" perceptions of value;
2. Using ideal points derived from perceptual maps as the dependent variable and conjoint derived utility values as the independent variable;
3. Extensive applications in developing formal models of customer satisfaction;
4. In tracking studies to illustrate how the weights between levels of the relational chain change over time;
5. In advertising research to determine the "level of processing" where advertising is exerting its effect;
6. In business-to-business research to understand value chains and value adding;
7. To more fully understand and document difference in market segments. Here segment membership is a latent variable;
8. To relate price sensitivity and brand loyalty to both product and respondent attributes;
9. To develop the prediction equations that serve as the basis to virtual reality software-market simulation software that includes an extensive enough array of variables to more fully mimic a marketplace, unlike the familiar simulators which use only a few respondents and product features and therefore simulate only a small comer of reality.
A final word of caution. There are now two publicly available packages for structured equation modeling: LISREL and EQS. Both require a pretty good level of familiarity with the concepts of SEM and statistical methods. Both have the ability to quickly solve meaningless models! Anyone interested in doing structured equation modeling is well advised to avail themselves of training; the technique is not too tolerant of errors and has not developed to the point where one can do a "canned" structured equation model. Nonetheless, in the right hands, SEM provides a powerful statistical technology for building bridges between seemingly disparate databases and going "behind" the numbers to understand the psychological context which gave rise to the particular numbers.
