Editor's note: Albert Madansky is vice president of the Analytical Group Inc., a Scottsdale, Ariz., research firm, and H.G.B. Alexander Professor Emeritus of Business Administration Booth School of Business, University of Chicago. He can be reached at albert.madansky@chicagobooth.edu.
The choice of products to be marketed from among a larger set of possible products is one that marketers face regularly. To help select those products to be marketed, two computations algorithms have been set forth, TURF (total unduplicated reach and frequency; see, for example, Cohen, 1993) and Shapley value (see, for example, Conklin and Lipovetsky, 1999, 2005). This article compares the two algorithms and suggests some shortcuts which are less computationally onerous and will produce roughly equivalent results.
TURF and Shapley value
Suppose we have n products and wish to select m of them such that the reach of the m products is maximum. There are t = n!/m!(n-m)! possible selections of m products out of n. What TURF does is look at all t combinations of m products and selects the one combination that maximizes the reach. To get a sense of the magnitude of t, we note that when n=17 and m=6 then t=12,376. But our firm has had requests for TURF analyses for situations as large as n=80, m=11, which meant searching for a maximum among 10,477,677,064,400 combinations.
The application of the Shapley value to this kind of data takes a different approach. It starts with the reach of the combination of all n products. It then proceeds to allocate that reach across each of the products in a manner that reflects the relative contribution of each product to the total reach. Advocates of the use of the Shapley value in selecting m out of n products would select the m products with the highest Shapley values.
In order to calculate the Shapley value one must look at the reaches of all combinations of products, from m=1 to m=n. This involves the computation of 2n reaches. When n=80, then, regardless of the number m of products to be selected, one would have to calculate the reaches of 1,208,925,819,614,630,000,000,000 combinations of products. And when n=17, one would have to calculate the reaches of all 131,072 combinations, as compared with the 12,376 combinations required for the use of TURF when m=6.
To illustrate the difference in the selections of the two approaches, I use a slightly modified data set from that used in an example by Conklin and Lipovetsky, 2005. In my data set there are 278 respondents with n=5 products, which we will dub A, B, C, D and E. The reach of all five products (r(ABCDE)) is 132 (or 47.5 percent). The individual reaches are: r(A)=78, r(B)=70, r(C)=73, r(D)=80, and r(E)=72. Thus the order of the products based on individual reaches, from high to low, is
D > A > C > E > B.
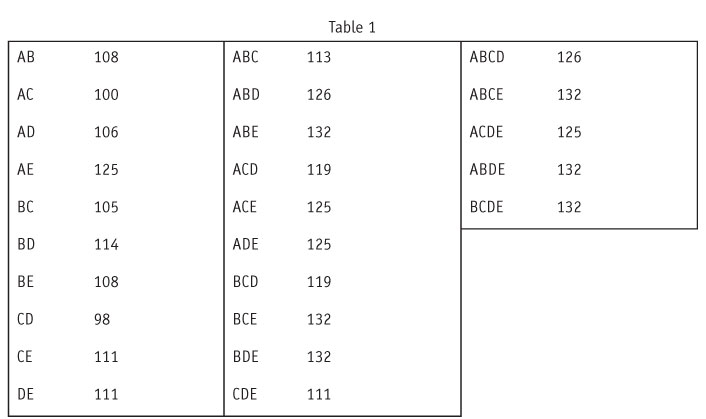
Table 1 presents the reaches of all pairs, triples and quadruples of products.
Let m=2. Then, based on this table, the pair with the highest reach is AE, where r(AE)=125, which is what TURF would have selected.
The Shapley values of the five products, along with the Shapley value percentage of r(ABCDE) for each product, are the shown in Table 2.
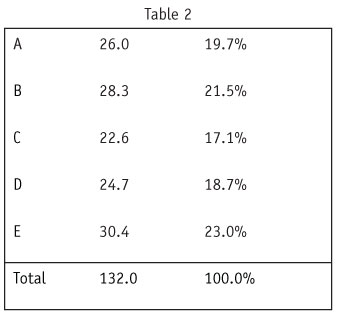
Thus the order of the products based on the Shapley values, from high to low, is
E >B >A >D >C.
Then, based on this, the pair with the highest Shapley values would be EB, with a reach of 108. This is because E and B provide, using the Shapley criterion, the most to the combined reach of all the five products. This, however, may not be an appropriate criterion for the marketer.
We can ratchet this argument backward to look at the case m=1. Then TURF (and common sense) says that the product to select if one had to select only one product is D, with a reach of 80, and not E, the product with the highest Shapley value, with a reach of 72. Yes, based on the Shapley criterion, Product E contributes most to the total reach of ALL five products. But, as Damon Runyon once said, “The race is not always to the swift, nor the battle to the strong, but that’s the way to bet.” If one has to go with one product, one should go with the one with the highest reach.
Stepwise TURF and main-component Shapley value
Given the enormity of the number of combinations one must assess in using TURF or Shapley value in determining product mixes, our firm has devised variants – stepwise TURF and main-component Shapley value – which greatly decrease the number of computations required to use these methods and generally produce the same results.
Stepwise TURF is patterned after the logic underlying stepwise regression. Stepwise TURF selects as its first product the one with the largest reach, say P1. Given that selection, it then looks at the n-1 remaining products and finds that product which, coupled with P1, produces a pair of products with highest reach, say P2. At the next step it looks at the n-2 remaining products and finds that product which, coupled with P1 and P2, produces a triple of products with highest reach, say P3. This process is followed until m products have been selected, at which point the m products are P1, P2, … , Pm. The number of reach combinations calculated in stepwise TURF is then n + (n-1) + (n-2) + … (n-m) = [n(n+1)-m(m+1)]/2. So even in the n=80, m=11 example cited earlier the number of reach combinations is 3,174, much smaller than the 10,477,677,064,400 combinations required by TURF.
To illustrate this process on the above data, stepwise TURF would first select Product D. It would next select Product B, because the reach of DB is greater than the reach of any other product coupled with D. This stepwise TURF would not find the optimum pair, because r(DB) is 114 whereas the optimal pair is AE, with a reach of 125.
As is the case in stepwise regression, stepwise TURF does not always lead to the absolute best set of m products. But, both because of its computational ease and because it follows the “Damon Runyon dictum” for m=1, it is a recommended approach when one has large TURF computations.
Main-component Shapley value
The formula for Shapley value (equation 3 of Conklin and Lipovetsky, 2005) is
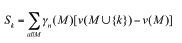
where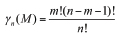
so that g=1/n when m=0 and when m=n-1, g=1/n(n-1) when m=1 and m=n-1, and with each increase in m g is of the order of 1/n times the predecessor value of g. Thus the greatest weights in the computation of Sk are for the first and last terms of the equation, those related to the single reach of each product and the contribution of that product to the reach of all n products. I illustrate this with an example (Table 3) for n=17.
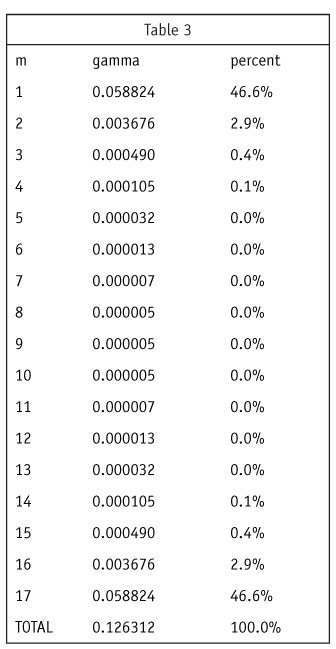
Note that the computations for m=1 and m=17 together get 93.2 percent of the weight in the computation of the Shapley value. So a main-component Shapley value computation would be based only on the first and last terms in the sum, both simple computations.
REFERENCES
E. Cohen, “TURF analysis.” Quirk’s Marketing Research Review (June/July 1993) 10-13.
W. M. Conklin and S. Lipovetsky, “A winning tool for CPG.” Marketing Research (Winter 1999/Spring 2000) 23-26.
W. M. Conklin and S. Lipovetsky, “Marketing decision analysis by Turf and Shapley value.” International Journal of Information Technology & Decision Making, 4(1) (2005) 5-19.
