Editor’s note: William M. Briggs is a statistical consultant based in New York.
There is a story about a marketing statistician who was asked by his mother what he was doing. “Modeling for Victoria’s Secret,” he said. “You’re doing no such thing!” she said. She was shocked. She shouldn’t have been, because classical statistics is a lot like a modeling lingerie.
A common experience many readers, especially of the male type, have of the Victoria’s Secret catalog is to marvel at how well the models exhibit their wares. A reader, surely fixated on fashion, might closely examine a photograph and say, “This model appears ideal. Her clothing fits perfectly.” Some especially attentive viewers can tell you the measurements of the garments down to the nearest fraction of an inch. They look at a model and announce, “She must not have got that outfit off the rack because there’s almost no chance a ready-made garment would have fit that well. It must have been made for her.” Yet, knowing this, they still buy the clothing hoping that it will do for them - or a close associate - exactly what it did for the model.
To prove the statistical marketing analogy, consider this typical scenario. Data to answer the question, “What factors are associated with overall product satisfaction?” are collected. The data is form-fit to a model. Certain data are tossed and said not to fit well; only the most flattering variables are kept. Those remaining are scrutinized. Assiduous statisticians comment on how well these variables fit the model, and state measurements of this fit. They say, “There’s no way our data could fit our model by chance. Look how beautiful it is!” They tell their clients of their success, and the clients go on to use the fit of this data on this model and hope that the fit will look as good in real life.
Undiscovered secret
The business of classical statistics, then, is judging how well data fits models. But there is an alternative to this practice called predictive inference. Its methods have been around for some time, but they are the great undiscovered secret of statistical methodology. Continuing the analogy: a predictivist would not ask how well a garment fit a Victoria’s Secret model but would ask how well that clothing might fit his inamorata.
Predictive methods use data that we have in hand (old data) to say things about data which will be collected in the future (new data). Think of it this way: we know everything there is to know about our old data, do we not? We know, for example, what percentage of women answered our surveys, we know how old they are, what products they bought, which they eschewed. And we know these things with 100 percent certainty. I often ask statisticians what I swear is a non-trick question - and it almost always stumps them. Suppose a client commissions a survey that finds 300 women and 200 men bought Product A. I ask, “Given this data, what is the probability that more women than men bought Product A?”
Ask this to a civilian and they respond, “Obviously, the probability is 1, or 100 percent, because 300 women bought Product A and only 200 men bought it, and 300 is certainly more than 200.” This is the right answer.
But statisticians bypass the simple question and substitute it for another difficult, self-imposed query, which they refuse to answer without being provided more information. “You need to tell us how many women and men were offered the opportunity of buying.” Say 1,000 of each; that is, 1,000 women and 1,000 men had the chance to buy.
This starts them calculating. Invariably, a chorus will call out something like, “The parameter estimates are 0.30 and 0.20. The p-value in a z-test is pretty small, say, p < 0.001. We reject the null hypothesis that the proportion of women and men who bought the product is equal. We conclude that the proportions are different!” Parameters? P-values? What is all this?
Future customers
The client who commissioned our study wanted not only to know about the people surveyed, he was curious about future customers, too. But suppose his interest was solely in those 2,000 original people, then he would be done. He wouldn’t need any statisticians, either, because he could answer any question he had about his data just by counting. How many women bought A? Just count. How many buyers were men older than 25? Just count.
We would instead like to use the old data to quantify uncertainty of our client’s entire universe of customers. Then we could answer questions like, “Given our sample, what is the probability more women than men in the future will buy Product A?”
Predictive statistics directly answers questions like this. Or, for example, like, “What is the probability that future shoppers will be more satisfied with Product B?” Notice that these are questions about observable data - amounts, counts, dollars.
Classical statistics cannot make direct statements about observable data like predictive statistics can. Instead, its focus is entirely on probability models, which are mathematical formulas that require for their existence strange entities called parameters. The mean of a normal distribution is a parameter, for example. Parameters are hidden, unknown and unknowable numbers that must be plugged into models before they work.
Even though parameters are unknowable, there are ways to guess their values. After guessing, we can calculate p-values, which are indirect measures of model fit. In fact, all talk of null and alternate hypotheses, etc., is nothing but statements of how well the probability model fit the old data - the old data which we already know all about. Even stronger, these statements are conditional on suppositions about the hidden parameters, and not about the observable data - a fact about which most are unaware. This is why statistics is confusing to most people: It is confusing!
Results are agnostic
Predictivist procedures also use probability models, but its results are agnostic about parameters, which never appear in its answers. Often, predictivist and classical methods use identical models, but the classical methods stop after making guesses about parameter values, while the predictivist methods continue on to make probability statements about future observable data.
The classical procedure ends with, “Given the parameters for men and women buying Product A are equal, the probability of seeing a test statistic larger than the one we got is 0.0001” - which is the correct, but difficult to remember, definition of a p-value. The predictivist answer is more informative: e.g., “Given the data, the probability that twice as many women than men will buy is 9 percent.” Predictivist methods can answer any question about the observable data a client might have.
P-values give highly inflated views of the strength of fit, too. For example, the p-value in our buying example is 0.000003 - which sounds like women and men are worlds apart. But the predictivist probability of the next woman buying and the next man not buying Product A is only 28 percent! This over-certainty arises because it is easier to be surer of parameter values than it is of actual observations.
Another example is provided in Figure 1. Two groups were polled about overall satisfaction (a number between 0 and 100). Group 2 was on average 25 points higher than Group 1. The classical 95 percent confidence interval of that difference is in green, where it appears we have good evidence Group 2 is higher. However, this confidence interval is for the difference in group parameters.
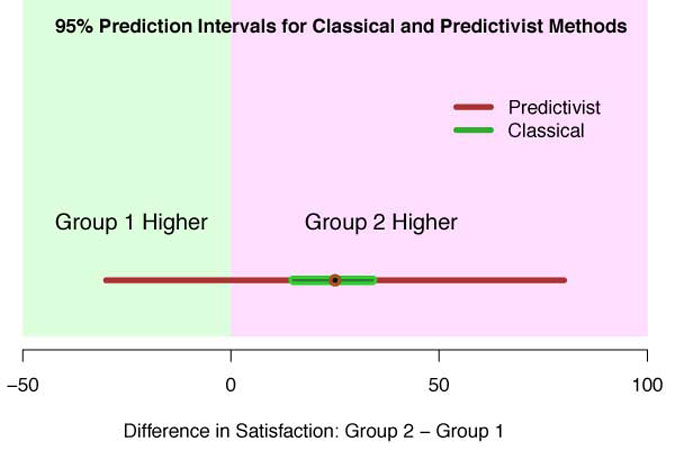
The predictivist method instead asks, “What is the range of actual differences in satisfaction scores I’m likely to see in future groups of people?” This range (in red) is much larger than the interval for the difference of parameters: it even shows there is a good chance Group 1 has higher scores!
When people first see this example - which is a typical one: predictivist intervals are always wider than classical ones - they complain that the predictivist interval is too wide, and that the decision about which group had higher ratings is easier to make classically. This is true: but remember the predictivist interval is a statement about real data we’ll actually see. And we are not after easy decisions, but correct ones.
Excessive certainty can be costly. In the buying example, suppose the client wants to allocate an advertising budget according to the statistical findings. Using classical methods might cause him to ignore males completely, while the predictive-inference findings suggest that while it’s likely more women than men buy, it’s not overwhelmingly probable that this will be true in the future.
Training has been limited
There are matching predictivist procedures for each classical method: regression, PLS, ANOVA, etc. So why aren’t predictivist methods used more often? Mostly because training for them has been limited, thus many statisticians aren’t familiar with the philosophy upon which these new methods are built. Luckily, this is changing as new books and classes appear regularly. Further, predictivist statistical methods are now available in packages like R, Sawtooth, WinBUGS and SAS.
They are no panacea, however, and can’t be used for every application. And you can still make a mistake using them - but not the dangerous mistake of being too sure of yourself.
