Editor's note: Mike Grigsby is vice president, strategic business analysis, at TargetBase, an Irving, Texas, research firm.
Retailers send out too many discounts. They give away too much margin. They know this but they do not know what to do about it. They have no way to analytically ascertain who is sensitive to price and really does need a discount and who is not or whether price sensitivity is differentiated by product categories or by time period.
The general approaches to pricing (for an existing product) are from marketing research and tend to be survey-based. The insights gained from those instruments are self-reported and seem self-serving. If behavior from a transactional database can be collected (actual purchases responding to actual price changes) then elasticity modeling can be carried out. This modeling will calculate price sensitivity (by product by time period) and strategic insights can be given in terms of maximizing net revenue.
As part of a test, this transactional data was collected for a specialty retailer and elasticity-modeling was performed. Price sensitivity was estimated by major product categories by quarter. Knowing this, a marketer could increase or decrease the price of these categories to take advantage of different sensitivities by quarter in order to maximize net profit.
An in-store field test was set up, in three increasingly wider designs. The results of the first showed products in the test stores was higher than the net revenue of the same products in the control stores by over 22 percent. The second design had test products outperforming control products by 14 percent and the last design had test products outperforming control products by 9 percent.
As mentioned, the client in question is a specialty retailer with over $1 billion in annual revenue, over 1,000 stores and over 10,000 employees. The previous year this retailer had a difference between gross and net revenue of about 26 percent. Since its products were non-discretionary – nearly hedonistic – requiring a deep discount in order to purchase seemed unlikely.
Generally, discounts were not differentiated. As in most retail organizations, merchandisers rule the world. Merchandisers buy products and forecast when they’ll have stock-outs. They do not want inventory on hand. So the level of (in-store) discounts and markdowns is all about making the stock-out meet the forecast, either at the month or quarterly end. Marketing communications (including offering coupons) is about getting customers into the store.
Therefore, the firm wanted a way to maximize the probability of purchase while minimizing the amount of margin given away. This required targeting. While not personalized at the customer level (yet), this stage was about finding out which products were more/less sensitive and when. That is, does Product X tend to be more sensitive to price in Q3 as opposed to Q1? If the answers to any of those questions are yes then a discounting (optimizing) strategy can be implemented.
Four approaches to pricing
Generally, there are four approaches to pricing. The first three of these are based on marketing research and use a survey method to generate the data. A primary research survey can be designed and administered. But this is, as are all survey-based tools, self-reported and self-serving. The second common approach is the Van Westen-dorp pricing analysis system. This survey generates two graphs: the percent of respondents who say the product in question is priced so high they would not buy and the percent of respondents who say the price is so cheap they would not buy. The intersection of these two lines is purported to be “optimal price.” Thirdly is conjoint. While this is about choices (considered jointly) it is not consumers choosing in a real economic environment. It is artificial and/or contrived.
The last approach is elasticity modeling. This data comes from a transactional database. This is real consumers responding to a real choice in a real economic environment. All of the swirling issues of competitive pressure and advertising awareness and satisfaction and loyalty, etc., are bundled together in that purchasing-related decision. This will give an accurate measure of price sensitivity.
Discount too much
Elasticity modeling is of utmost importance, especially in retail industries. Retailers typically discount too much (and they know it) but they have no real way to target or test or understand (quantitatively) how to wean themselves off the drug. It is clear some customers do need a (deep) discount in order to maximize probability to purchase and it is also usually the case other customers (particularly for some product categories and/or at some times of the year) do NOT need a (deep) discount in order to purchase. It is the task of marketing analytics to understand and exploit this sensitivity to price.
That’s why, for an existing product, if a database is available that tracks customers’ actual purchases and responses to actual marketing communications and merchandisers’ markdowns offering actual changes in price, elasticity analysis is the only real solution. And it is actually cool.
Elasticity, as such, is an unfortunate term. It’s a little awkward, cumbersome and not exactly even accurate. The right word is “sensitivity.” The concept is a measure of how sensitive is an output variable (typically units) to a change in some input variable (and in this case that’ll be price). That is, given a percent change in price what is the resultant percent change in units?
We like the idea of elasticity because it is what mathematicians call a pure number: It is without dimension or scale. This is because elasticity is a marginal function over an average function.
There are two kinds of elasticity: elastic and inelastic; that is, sensitive and insensitive. When price changes by X percent and units change by greater than X percent, we say units are sensitive to price. When price changes by X percent and units change by less than X percent, we call this insensitive to price. Note that the relationship between units and price is always inverse, that is, negative. When price goes up units will go down. That is the only law in all of economics, the law of demand. Because it is always calculated as negative we usually ignore the sign. That is, we always take the absolute value. If the elasticity is < 1.00 we call it inelastic and if it is > 1.00 we call it elastic.
While price has an impact on units, the real magic of elasticity is the effect on total revenue. Note that total revenue = price * units. In an inelastic demand curve total revenue follows price. That means if you want to increase total revenue you must increase price. In an elastic demand curve, total revenue follows units. If you want to increase total revenue you must decrease price. By price I mean (and will always mean) net price; that is, after discounts.
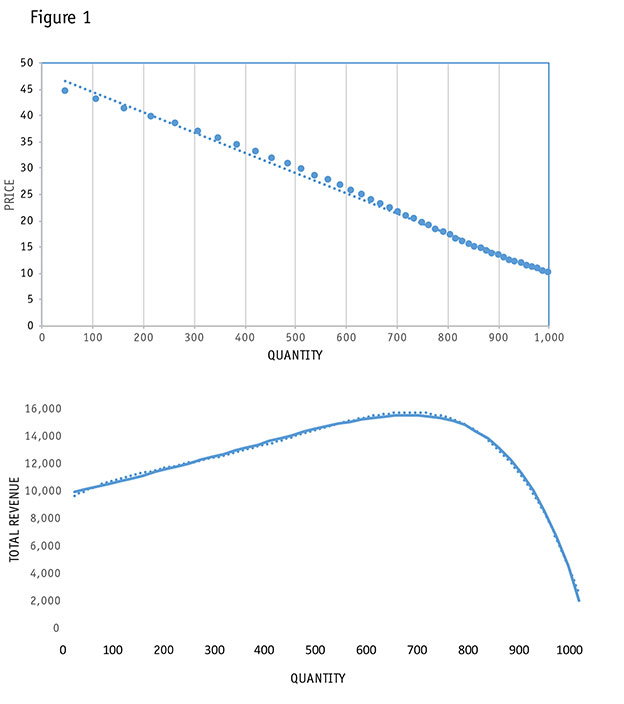
Note Figure 1. The top graph is the typical price-unit demand curve. It displays the inverse relationship as expected. Price is on the vertical axis and units is on the horizontal axis. The bottom graph shows units and total revenue. Note that at the higher end of the units axis total revenue can only increase if there is a price increase. That part of the demand curve is inelastic. The opposite is true at the lower end of units which have the higher end of prices. In order to increase total revenue price must be decreased. That is the elastic portion of the demand curve.
From mathematical to statistical
To understand how modelling elasticity works, it’s important to go from the mathematical to the statistical definition. When first exposed to elasticity the simple idea was demonstrated with point elasticity, that is, the elasticity between two points.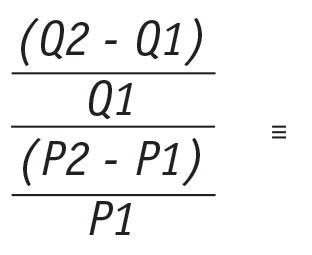
After point elasticity we are next exposed to arc elasticity, the elasticity of a larger part of the demand curve.
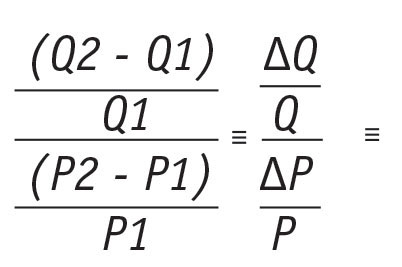
That is, differences in the two points from quantity, mathematically becomes the change in quantity and the difference in the two points from price mathematically become the change in price. This change in Q over Q divided by change in price over P is the arc.
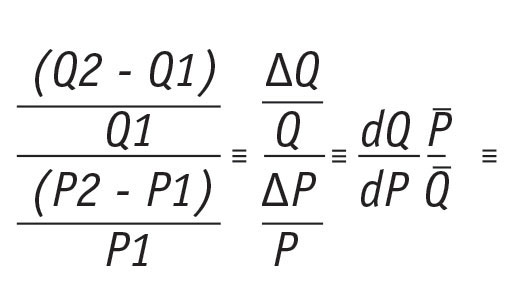
Now comes the fun part. Change in Q over change in P is the marginal function. How Q changes as P changes shows an average slope of the whole (demand) function. This average slope in mathematics is called the derivative of Q with respect to P. So mathematically, elasticity is the marginal function over an average function, or the derivative of Q with respect to P multiplied by average P over average Q. Here comes the kicker.
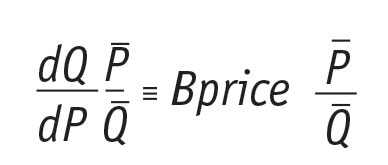
The average slope in mathematics is called the derivative and it is measured without error, all points on the function exactly equate to the function. In statistics the function is not measured without error but includes a random error term, e. But the concept of average slope in ordinary regression is called the coefficient. So the coefficient in statistics is analogous to the derivative in mathematics. In a demand model where quantity is the dependent variable and price is the independent variable, to calculate elasticity requires multiplying the coefficient of price by average price over average quantity. Voila!
Very insensitive to price
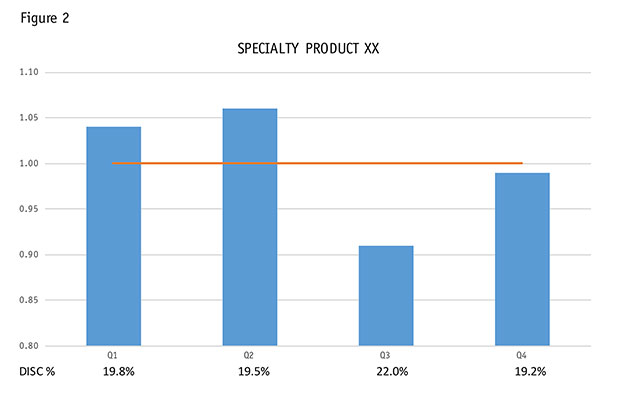
So elasticity modeling was done by product category by quarter. The chart in Figure 2 shows two such (extreme) results. Product category XX is shown as very insensitive to price. Below the chart is detailed the average discount rate for this product at that quarter. This product has the highest average discount rate even though it is the least sensitive to price. This is exactly the wrong strategy! The customers who buy Product XX are NOT sensitive to price yet they get the largest discount. (Note that they will take the discount, they just do not need the discount.) A discount of a few percentage points lower can save millions of dollars in margin. Even if this product is used as a loss-leader and a large discount is given as a “starter basket,” etc., the discount is probably far too high. The recommendation would be to test decreasing discounts, lower and lower, until it makes a difference.

Essentially the opposite story is told in Figure 3 with Product YY. This product is very sensitive to price but is given the lowest average discount. To buy more customers tend to need a larger discount.
‘How cool!’
So the company saw the results of the model and said, “Wow, how cool!” Actually it did not say that, especially the merchandisers. Again, in retail, as mentioned before, merchandisers rule the world. The last thing they wanted was for marketing to mess with prices. The merchandiser’s job is to buy inventory and forecast the stock outages to end at a certain time, e.g., end of month or end of quarter, etc. They would be nervous about marketing messing around with something that may affect their forecasts.
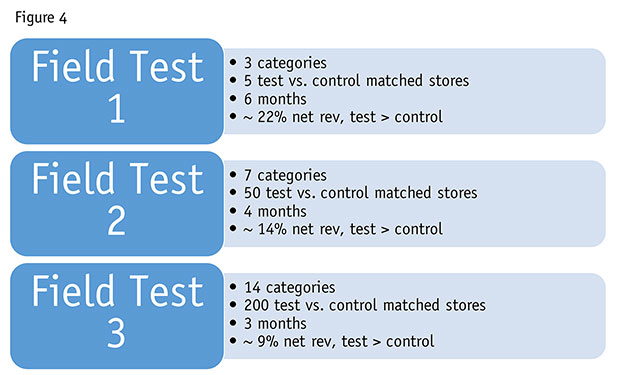
A field test was designed (Figure 4). The first one used three categories (those at most risk with strongest opportunities) and matched five test to five control stores. After six months the net revenue of the products chosen of the test stores outperformed the net revenue of the control stores by over 22 percent! Note that a test result of 2.2 percent would have been seen as positive and significant. So the retailer broadened and widened the second test. This now included seven categories and 50 stores. The net revenue of the products chosen of the test stores outperformed the net revenue of the control stores by over 14 percent, over a four-month period. Not quite convinced, a third test was implemented, this time using 14 categories in 200 stores and in three months the net revenue of the products chosen of the test stores outperformed the net revenue of the control stores by over 9 percent!
What can be done with this information? It obviously can be used to create pricing strategies by category by season. That is, both marketing communications and store merchandisers can raise/lower net price by adding/subtracting discounts, offers, markdowns, etc. This can be at the overall level but margin can be optimized by manipulating discounts by product categories.
It also has implications for marketing and advertising and messaging/bundling. That is, given that we know which products consumers are price-sensitive to, a retailer could create offers that were so compelling that consumers might buy more of the same product or, more importantly, more of different products with richer margins.
Pull the plug
I have done elasticity modeling myself dozens of times, for various industries in widely different competitive arenas. It always works. There is always opportunity. Note also that it is with little risk. Simply monitor the net revenue and if the test products are not performing just pull the plug. Stop the test. That’s why elasticity modeling is recommended: It mathematically has to work, comes with nearly zero risk and there is a high probability of returning positive gain in net revenue.
